Today is our topic of discussion Area of triangles .
Area of triangles
We know we get the region of a triangle if we connect straight lines with three different points that are not lying on the same straight line. That region of the triangle may be different respective of the side and the angle.
In this part we will be able to determine the area of any triangle by finding the sides of the triangle with the help of only one formula. With the help of this same formula, by dividing any quadrilateral into the two triangles, the determination of the area of the region of the quadrilateral will be possible. In this case we will determine the area using the perimeter of the triangle (the sum of the lengths of the sides) and the length of the side.
To determine the area of a triangle shaped or angle-shaped land, the method i.e. by the length of side, is very important. So, it is very useful in determining the area of the land. It is said, as the reason, if the coordinates of the vertices of the triangular or quadrangular land are not known or are not possible to know but if the coordinates are known, we will be able to determine the area more easily. In this part we shall determine the area of a triangle or a polygon by these two methods.
Method 1: Determination of the Area Using the Length of Sides and Perimeter
The determination of the Area:
A triangle ABC has been shown in the adjacent figure. A(x1,y1), B(x2, y2) and C(3, 3) are three different points and AB, BC and CA are the three sides of the triangle. With the help of the formula of determining distance, it is possible to determine easily the lengths of the sides AB, For example:
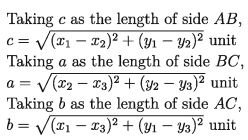
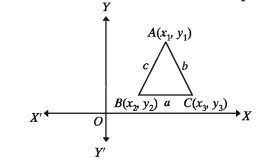
Now taking the perimeter of the triangle as 2s,
2s = a + b + c [Perimeter = the sum of the lengths of the three sides.]
So, s = 1/2 (a + b + c) unit, Here s is the half of the perimeter of the triangle
We can easily determine the area of any triangle with the help of s and a, b, c.
T
The Formula for Determining the Area of Triangular Region
If in ABC, the length of the side AB is c the length of the side BC is a and the length of the side CA is b and perimeter is 2s. So the area of triangle ABC is sqrt(s(s – a)(s – b)(s – c)) square unit [The proof has been given in the part of mensuration of the Mathematics book of class 9-10. The students should check out the proof.]
By the following examples, the use of the formula will be easily understood.
Observation:
There are different formulas for determining the area of different triangles but here we shall able to determine the area of any triangle with the help of only one theory.
Method 2: Determination of the Area Using the Coordinates of the Vertices
By this method the area of a triangle can be determined very easily with the help of the coordinates of the three vertices of a triangle. If the coordinates of the vertices of any polygon are known, the area of the polygon can also be determined in the same way.
However, in real life, it is not possible to use this method. This is because if we want to determine the area of a land and if the shape of the land is triangle or square, the area can not be determined by this method since the coordinates of the angular points are not known or are not possible to know.
But we can easily measure the length of the sides of a land and determine the area by the Method 1. So, it is necessary for the students to have conceptions about both methods. Method 2 for determining the area of triangles and polygons is discussed below with examples:
The General Formula of Determining the Area of a Triangle:
Let, A(x_{1}, y_{1}) , B(x_{2}, y_{2}) and C(x_{3},y_{3}) be the three vertices of the triangle ABC. Like the figure similar to below, the points A, B and C are arranged in anti-clockwise order.
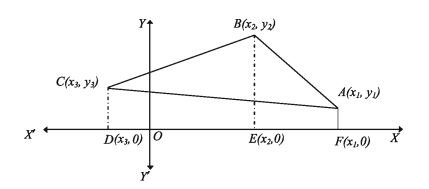
From the figure we get,
Area of polygon ABCDF = area of triangle ABC + area of trapezium ACDF. = area of trapezium ABEF + area of trapezium BCDE.
Therefore we get,
Area of triangle ABC area of trapezium ABEF + area of trapezium BCDE
area of trapezium ACDF.
Area of the Triangle ABC

Where in the side of multiplication as the positive sign we get x_{1}y_{2} + x_{2}y_{3} + x_{3}y_{1} and as the negative sign we get – x_{2} y_{1} – x_{3}y_{2} – x_{1}y_{3}
See more:

3 thoughts on “Area of triangles”