Today is our topic of discussion Laws of Vector Addition.
Laws of Vector Addition
Just like arithmetical addition, in vector addition commutative, associative and cancellation law can be used.
Commutative law:
For any two vectors u, v, we get u + v = v + u
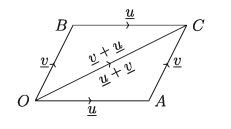
Proof:
Let OA = u and OB = v . Draw the parallelogram OACB and its diagonal OC. OA and BC are equal and parallel. Also OB and AC are equal and parallel.
OC = OA + AC = u + v ;again, OC = OB + BC = OB + OA = v + u
u + v = v + u Therefore, addition of vectors obeys the commutative law.
Associative law of addition of vectors:
For any three vectors u, v, w we have
(u + v) + w = u + (v + w)
Proof:
Let, OA = u , AB = v , BC = w , i.e. v is drawn from the terminal of u and w is drawn from the terminal point of v. Join O, C and A, C.
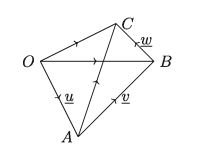
Then (u + v) + w =( OA + AB )+ BC = OB + BC = OC
Again, u + (u + w) = OA +( AB + BC )= OA + AC = OC
(u + v) + w = u + (v + w) Hence vector addition obeys associative law.
Corollary 1. The sum of three vectors represented by the three sides of a triangle taken in the same order is zero. In the diagram above, vec OB + BA + AO = 0
OA + AO =- AO + AO = 0
Cancellation law of addition of vector:
For any three vectors u, v, w, if u + v = u + w then, v = w
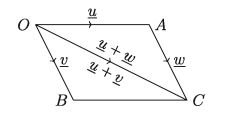
Proof:
As u + v = u + w u + v + (- u) = u + w + (- u) [Adding -u in both sides]
or, u – u + v = u – u + w i.e. v = w
Scalar multiple of a vector
If u is any vector and m is any real number, then what is understood by mu is explained here now.
1. If m = 0 then, mu = 0 or zero vector
2. If m ≠ then, the length of mu is equal to |m| times that of u and the supports of mu are same as that of u’s. And,
1) If m > 0 then direction of mu and that of u are same.
2) If m < 0 then direction of mu and that of u are opposite.
Note: 1) if m = 0 or u = 0 , then mu = 0 2 ) 1u = u, (- 1) u = – u
From the above definition, it is observed that, m(nu) = n(mu) = (mn)(u)
Both m, n > 0 both < 0, any one > 0 and the other < 0 , any one or both is zero -after considering all these case separately, the reality of the rule can be established. An Example of such cases is given below :
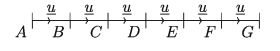
Suppose, AB = BC = u
AC is produced up to G, such that CD = DE = EF = FG = AB .
Then AG = AB+ BC + CD + DE + EF+FG: =u+u+u+u+u+u= 6u
Again, AG = AC + CE + EG = 2u + 2u + 2u = 3(2u)
And AG = AD + DG = 3u + 3u = 2(3u)
2(3u) = 3(2u) = 23(u)
Note: If the support lines of two vectors are alike or parallel, then one can be expressed as scalar multiple of the other.
In reality, if AB ||CD then, vec AB =m vec CD where,
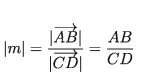
1) if m > 0 , vec AB and vec CD are alike in direction, 2) if m < 0 , vec AB and overleftrightarrow CD are unlike in direction,
Distribution laws concerning scalar multiples of vectors
If m, n are two scalars and u and v are two vectors then
1. (m + n)u = mu + nu
2. m(u + v) = mu + mv
Formula 1. (m + n) * u = m * u + n * u
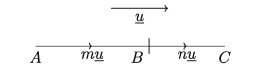
Proof:
If m or n is zero, then the law is obviously true. Suppose both m and n are both positive and vec AB = mu .. |AB |= m|u|
See more:
