Today our topic of discussion is Relations of Mathematics.
Relations of Mathematics

Relations
We know Dhaka is the capital of Bangladesh, New Delhi is of India and Bangkok is of Thailand. There is a relation between capitals and countries. This is country- capital relation. This relation can be expressed as a set in the following way:
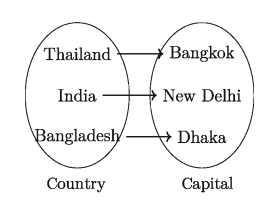
That is country-capital relation = {(Bangladesh, Dhaka), (India, New Delhi), (Thailand, Bangkok)}.
If A and B are two sets then, nonnull subset R of ordered pairs of their Cartesian product A x B is said to be a relation from the set A to the set B. Here set R is a subset of the set AX B. That is, RC AXB
Example 15. Let us assume that A = {3, 5} and B = {2, 4} AB = {3, 5}{2, 4} = {(3, 2), (3, 4), (5, 2), (5, 4)}
R ⊆ {(3, 2), (3, 4), (5, 2), (5, 4)}
when for an element of set A and an element y of set B (x, y) in R, then it is written z Ry and read that z is related to y, that is, z is related to y using relation R.
If x > y_{1} then R = {(3, 2), (5, 2), (5, 4)} and if x < y then R = {(3, 4)}
Again, if there is a relation from set A to set A, that is, R ⊆ A then R is a relation of A.
If x ∈ A,y ∈ B is related, then the nonempty subset of ordered pairs (x, y) is called relation.
Example 16. If P = {2, 3, 4} , Q = {4, 6} and for elements of P and Q a relation y = 2x exists, then find the relations.
Solution: Given, P = {2, 3, 4\} and Q = {4, 6}
According to the question R={ (x, y) 😡 ∈ P,y in Q and y = 2x ) Here, PQ = {2, 3, 4}{4, 6} = {(2, 4), (2, 6), (3, 4), (3, 6), (4, 4), (4, 6)} . R = {(2, 4), (3, 6)}
The required relation is {(2, 4), (3, 6)}
Example 17. If A = {1, 2, 3} B = {0, 2, 4} and elements of A and B have the relation x = y – 1 find the relations.
Solution: Given, A = {1, 2, 3} , B = {0, 2, 4}
According to the question, relation R={ (x, y) : A, y ∈ B and x = y – 1 }
Here, AB = {1, 2, 3}{0, 2, 4}
={(1, 0), (1, 2), (1, 4), (2, 0), (2, 2), (2, 4), (3, 0), (3, 2), (3, 4)}
R = {(1, 2), (3, 4)}

Work: If C = {2, 5, 6} , D = {4, 5} and the relation x <= y holds between elements of C and D, find the relations.
