Today our topic of discussion is Simple simultaneous equations.
Simple simultaneous equations

Simple Simultaneous Equations in Two Variables
For solving the mathematical problems, the most important topic of Algebra is equation. In classes VI and VII, we have got the idea of simple equation and have known how to solve the simple equation in one variable. In class VIII, we have solved the simple simultaneous equations by the methods of substitution and elimination and by graphs.
We have also learnt how to form and solve simple simultaneous equations related to real life problems. In this chapter, the idea of simple simultaneous equations have been expanded and new methods of solution have been discussed. Besides, in this chapter, solution by graphs and formation of simultaneous equations related to real life problems and their solutions have been discussed in detail.
At the end of the chapter, the students will be able to-
⇒ verify the consistency of simple simultaneous equations in two variables.
⇒ verify the mutual dependence of two simple simultaneous equations in two variables
⇒ explain the method of cross-multiplication.
⇒ form and solve simultaneous equations related to real life mathematical problems.
⇒ solve the simultaneous equations with two variables by graphs.
Simple simultaneous equations
Simple simultaneous equations means two simple equations in two variables when they are presented together and the two variables are of same characteristics. Such two equations together are also called system of simple equations. In class VIII, we have solved such system of equations and learnt to form and solve simultaneous equations related to real life problems. In this chapter, these have been discussed in more details.
First, we consider the equation 2x+y= 12. This is a simple equation in two variables.
In the equation, can we get such values of x and y on the left hand side for which the sum of twice the first with the second will be equal to 12 of the right hand side; that is, the equation will be satisfied by those two values?
Now, we fill in the following chart from the equation 2x+y=12:
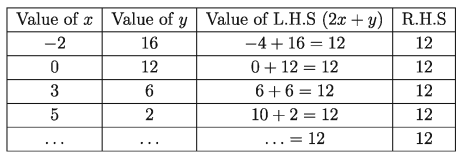
The equation has infinite number of solutions. Among those, four solutions are: (-2, 16), (0, 12), (3, 6), (5, 2).
Again, we fill in the following chart from another equation, x – y = 3
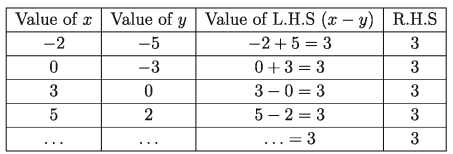
The equation has infinite number of solutions. Among those, four solutions are: (-2,-5), (0,-3), (3,0), (5, 2).
If the two equations discussed above are considered together a system, both the equations will be satisfied simultaneously only by (5, 2). Both the equations will not be satisfied simultaneously by any other values.
Therefore, the solution of the system of equations 2x+y= 12 and x-y-3 is (x, y) = (5,2).
Conformability for the solution of simple simultaneous equations in two variables
1) As discussed earlier, the system of equations [[2x + y = 12], [x – y = 3]] \ has unique (only one) solution. Such systems of equations are called consistent. Comparing the coefficient of x (taking the ratio of the coefficients) of the two equations, we get, 2/1 ≠ 1 -1 ; any equation of the system of equations cannot be expressed in terms the other. That is why, such systems of equations are called mutually independent. In the case of consistent and mutually independent system of equations, the ratios are not equal. In this case, the constant terms need not to be compared.
2) Now we shall consider the system of equations two equations be solved? [[2x – y = 6], [4x – 2y = 12]] \ . Can these
Here, if both sides of first equation are multiplied by 2, we shall get the second equation. Again, if both sides of second equation are divided by 2, we shall get the first equation. That is, the two equations are mutually dependent.
We know, the first equation has infinite number of solutions. So, the second equation has also the same infinite number of solutions. Such systems of equations are called consistent and mutually dependent. Such systems of equations have infinite number of solutions. Here, comparing the coefficients of x and y, and the constant terms of the two equations, we get, 2/4 = – 1/- 2 = 6/12 * (- 1/2)
That is, in the case of the system of such simultaneous equations, the ratios become equal.
3) Now, we shall try to solve the system of equations 2x + y = 12 ,4x + 2y = 5 .
Here, multiplying both sides of first equation by 2, we get, 4x + 2y = 24 second equation is, 4x + 2y = 5
subtracting, 0= 19 which is impossible.
So, we can say, such systems of equations cannot be solved. Such systems of equations are inconsistent and mutually independent. Such systems of equations have no solution.
Here, comparing the of x and y and constant terms from the two equations, we get, 2/4 = 1/2 ≠12/5
That is, in case of the system of inconsistent and mutually independent equations ratios of the coefficients of the variables are not equal to the ratio of the constant terms.
Generally, conditions for conformability of two simple simultaneous equations, such as, a1x + b1y = c1 , a2x + b2y = c2 are given in the chart below:
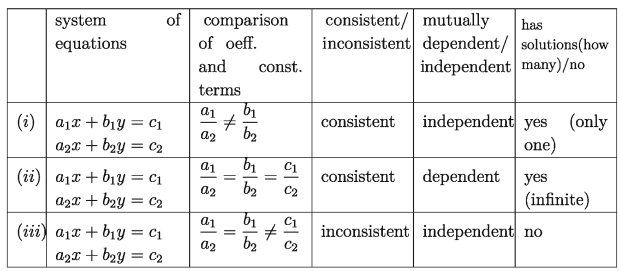
Now, if there is no constant terms in both the equations of a system of equations c1= c2 = 0 then from the table:
According to (i) if a1/a2 ≠ b1/ b/2 , the system of equations is always consistent and independent of each other. In that case, there will be only one (unique) solution. According to (ii) if a1/a2 = b1/ b2 the system of equations is consistent and dependent of each other. In that case, there will be infinite number of solutions.
Example 1. Explain whether the following systems of equations are consistent/ inconsistent, dependent/ independent of each other and indicate the number of solutions in each case.
1) x + 3y = 1
2x + 6y = 2
2) 2x – 5y = 3
x + 3y = 1
3) 3x – 5y = 7
6x – 10y = 15
Solution:
1) Given system of equations is:[x + 3y = 1],[2x + 6y = 2]
Ratio of the coefficients of x is 1/2
Ratio of the coefficients of y is 3/6 * or, 1/2
Ratio of constant terms is 1/2
∴ 1/2 = 3/6 = 1/2
Therefore, the system of equations is consistent and mutually dependent. The system of equations has infinite number of solutions.
2) Given system of equations is: 2x – 5y = 3, x + 3y = 1
Ratio of the coefficients of z is 2/1
Ratio of the coefficients of r is – 5/3
We get, 2/1 ≠ -5/3
∴ Therefore, the system of equations is consistent and mutually independent. The system of equations has only one (unique) solution.
3) Given system of equations is: 3x – 5y = 7, 6x – 10y = 15
Ratio of the coefficients of x is 3/6 or, 1/2
Ratio of the coefficients of y is or, – 5/- 10 or, 1/2
Ratio of constant terms is 7/15
We get, 3/6 = -5 /-10 ≠ 7/15
∴ Therefore, the system of equations is inconsistent and mutually independent. The system of equations has no solution.
See more:
