Today our topic of discussion is Rotational symmetry.
Rotational symmetry

Rotational symmetry
When an object rotates around any fixed point, its shape and size do not change. But the different parts of the object change their position. If the new position of the object after rotation becomes identical to the original position, we say the object has a rotational symmetry.
The wheels of a bicycle, ceiling fan, square etc. are examples of objects having rotational symmetry. As a result of rotation the blades of the fan looks exactly the same as the original position more than once.
The blades of a fan may rotate in the clockwise direction or in the anticlockwise direction. The wheels of a bicycle may rotate in the clockwise direction or in the anticlockwise direction. The rotation in the anticlockwise direction is considered the positive direction of rotation.
This fixed point around which the object rotates is the centre of rotation. The angle of turning during rotation is called the angle of rotation. A full-turn means rotation by 360°; a half-turn is rotation by 180°.
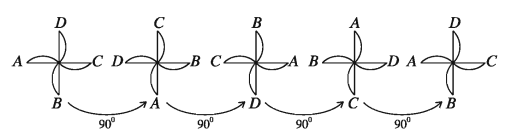
In the figure below, a fan with four blades rotating by 90° is shown in different positions. It is noted during a complete revolution in four positions (rotating about the angle by 90°, 180°, 270° and 360°), the fan looks exactly the same. For this reason, it is said that the rotational symmetry of the fan is order 4.
Here is one more example for rotational-symmetry. Consider the intersection of two diagonals of a square the centre of rotation. In the quarter turn about the centre of the square, any diagonal position will be as like as the second figure. In this way, when you complete four quarter-turns, the square reaches its original position. It is said that a square has a rotational-symmetry of order 4.

Observe also that every object occupies same position after one complete revolution. So every geometrical object has a rotational-symmetry of order 1. For finding the rotational-symmetry of an object, one needs to consider the following matter.
1) The centre of rotation
2) The angle of rotation
3) The direction of rotation
4) The order of rotational-symmetry
Line symmetry and rotational symmetry
We have seen that some geometrical shapes have only line symmetry, some have only rotational symmetry and some have both line symmetry and rotational-symmetry. For example, the square has four lines of symmetry as well rotational-symmetry of order 4.
The circle is the most symmetrical figure, because it can be rotated around its centre through any angle. Therefore, it has unlimited order of rotational of symmetry. At the same time, every line through the centre forms a line of reflection symmetry and so it has unlimited number of lines of symmetry.
See more:
