Area of Quadrilateral Region

Today our topic of discussion is Area of Quadrilateral Region.

Area of Quadrilateral Region

 

 

Area of Quadrilateral Region

1. Area of Rectangular Region: Let, the length of AB = a breadth BC = b and diagonal AC = d of rectangle ABCD. We know, the diagonal of a rectangle divides the rectangle into two equal triangular regions.

 

 

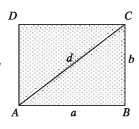
∴ Area of the rectangle ABCD 2x area of ΔABC = 2 * 1/2 * ab = ab perimeter of the rectangular region, s = 2(a + b) and observe that triangle ABC is right-angled.

∴A * C² = A * B² + B * C²

or, d² = a ² + b²

d = √(a² + b²)

2. Area of Square Region: Let the length of each side of a square ABCD be a and diagonal d. The diagonal AC divides the square region into two equal triangular regions.

 

 

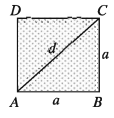
∴ Area of the square region ABCD = 2x area of

triangle ABC = 2 * 1/2 * aa = a² = (length of a side)² Observe that, the perimeter of the square region 4a and diagonal d = √(a² + a²) = √(2a²) = √(2) * a s =

3. Area of a parallelogram region:

a) Base and height are given: Let, the base AB = b and height DE = h of parallelogram ABCD. The diagonal BD divides the parallelogram into two equal triangular regions.

 

 

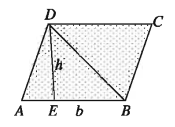
∴ The area of the parallelogram ABCD

= 2x area of triangle ABD = 2 * 1/2 * bh = bh

b) The length of a diagonal and the length of a perpendicular drawn from the opposite angular point on that diagonal are given:

 

 

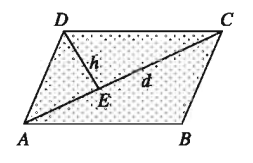
Let, in a parallelogram ABCD, the diagonal be AC = d and the perpendicular from opposite angular point D on AC be DE = h Diagonal AC divides the parallelogram into two equal triangular regions. ∴The area of the parallelogram ABCD = 2x area of ΔACD = 2 * 1/2 * dh = dh

4. Area of Rhombus Region: Two diagonals of a rhombus region are given.

 

 

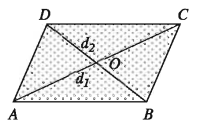
Let the diagonals be AC = d_{1} BD = d_{2} of the rhombus ABCD and the diagonals intersect each other at O. Diagonal AC divides the rhombus region into two equal triangular regions. We know that the diagonals of a rhombus bisect each other at right angles.

∴ Height of ΔACD = d2/2

∴ The area of the rhombus ABCD

d2 = 2x area of AACD = 2x2d2

5. Area of trapezium region: Two parallel sides of trapezium region and the distance of perpendicular between them are given. 

 

 

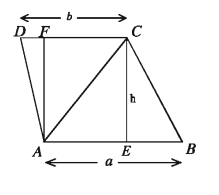
Let ABCD be a trapezium whose lengths of parallel sides are AB = a unit, CD = b unit and distance between them be CE = AF = h Diagonal AC divides the trapezium region = area of AABC+ area of AACD

ABCD into AABC and AACD. Area of trapezium region ABCD

= 1/2 * ABCE + 1/2 * CDAF = tilde 1 2ah + 1/2 * bh = tilde h (a+b) 2

Example 8. Length of a rectangular room is 3/2 times of breadth. If the area is 384 square metre, find the perimeter and length of the diagonal.

Solution: Let breadth of the rectangular room is z metre.

∴ Length of the room is 3/2 * x and area 3/2 * xx = 3/2 * x ² According to the question, 3/2 * x ²= 384or .. x = 16 metre. 3x²= 768 or, x² = 256

Length of the rectangular room = 3/2 * 16 = 24 metre and breadth = 16 metre.

∴ Its perimeter = 2(24+16) metre = 80 metre and length of the diagonal = √(24² + 16²) * metre = √(832) * metre =28.84 metre ( approx.)

The required perimiter is 80 metre and length of the diagonal is 28.84 meter (approx.)

Example 9. The area of a rectangular region is 2000 square meter. If the length is reduced by 10 metre, it becomes a square region. Find the length and breadth of the rectangular region.

Solution: Let length of the rectangular region be a metre and breadth y metre.

∴ area of the rectangular region is = xysq metre

According to the question, xy =2000…(1) and x – 10 = y (2)

Putting y = x – 10 in equation (1) we get,

x(x – 10) = 2000or, x² – 10x – 2000 = 0

or, x² – 50x + 40x – 2000 = 0 or, (x – 50)(x + 40) = 0

∴ x = 50or ,x=-40

But length can never be negative… x = 50

Now putting the value of x in equation (2) we get, y = 50 – 10 = 40

∴ The length of the rectangular is 50 and breadth 40 metre.

Example 10. There is a road of 4 metre width inside around a square field. If the area of the road is 1 hector, determine the area of the field excluding the road.

 

 

Solution: Let, the length of the square field is a metre.

∴ Its area is x² sq. metre

There is a road around the field with width 4 metre.

Length of the square field excluding the road = (x – 2 * 4) or, (8) metre.

Area of the square field excluding the road is = (x – 8)²

1. met re .. Area of the road=r2-(2-8)2 sq. metre

We know, 1 hector = 10000 sq. metre

According to the question, x² – (x – 8)² = 10000

or, x ² – x ²+ 16x – 64 = 10000

or, 16x = 10064

∴ x = 629

Area of the square field excluding the road

= (629 – 8)² * sq . metre = 385641 sq. metre = 38.56 hector (approx.)

The required area = 38.56 hector ( approx .) .

Example 11. The area of a parallelogram is 120 sq. cm and length of one of its diagonal is 24 cm. Determine the length of the perpendicular drawn on that diagonal from the opposite vertex.

 

 

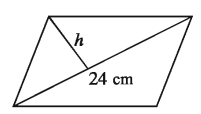
Solution: Let a diagonal of a parallelogram be d = 24cm and the length of the perpendicular drawn on the diagonal from the opposite vertex be h cm.

∴ Area of the h

As per question, dh = 120or, h = 120/d = 120/24 = 5 The required length of the perpendicular is 5 cm.

Example 12. The length of the sides of a parallelogram are wetre and 8 metre If the length of the smaller diagonal is 10 m, determine the length of the other diagonal.

Solution:

 

 

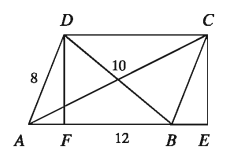
Let, in the parallelogram ABCD; AB = a = 12 metre and AD = c = 8 metre and diagonal BD = b = 10 metre Let us draw the perpendiculars DF and CE from D and C on AB and the extended part of AB respectively. Join C, A and D, B.

12+10+8

∴ Semi perrimeter of AABD, s = 2 metre = 15 metre. .. area of triangle ABD = √(s(s – a)(s – b)(s – c)) = √(15(15 – 12)(15 – 10)(15 – 8)) . sq. aetre = sqrt(15 * 3 * 5 * 7) * sq . metre = sqrt(1575) sq. metre 39.68 sq. metre (approx.)

Again, area of ΔABD = 1/2 * ABDF

or, 39.68 = 1/2 * 12DF or, 6DF = 39.68 .

Now, ABCE is a right-angled triangle.

DF = 6.61 (approx.)

∴ B * E ² = B * C² – C * E² = A * D² – D * F² = 8² – (6.61) ² = 20.31

∴ BE = 4.5 (approx.)

So, AE = AB + BE = 12 + 4.5 =16.5(approx.)

In the right-angled AACE

A * C² = A * E² + C * E² = (16.5)² + (6.61)² = 315.94

∴ AC = 17.77 (approx.)

The required length of the diagonal is 17.77 metre (approx.)

Example 13. The length of a diagonal of a rhombus is 10 metre and its area is 120 sq. metre. Determine the length of the other diagonal and its perimeter.

Solution:

 

 

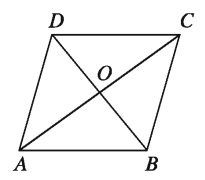
Let, the length of a diagonal of rhombus ABCD is BD = D d_{1} = 10 metre and another diagonal d_{2} metre. Area of the rhombus is = 1/2 * d_{1}*d_{2}*sq meter

As per question, 1/2 * d_{1}*d_{2} = 120 or, met.re. d_{2} = (120 * 2)/10 = 24

We know, the diagonals of rhombus bisect each other at right angles. Let the diagonals interset at the point O.

∴ OD = OB = 10/2 metre 5 metre

and OA = OC = 24/2 metre= 12 metre.

In the right-angled ΔAOD

A * D² = O * A² + O * D² = 12² + 5²

therefore AD = 13

∴The length of each sides of the rhombus is 13 metre.

The perimeter of the rhombus = 4 * 13 metre e = 52I metre The required length of the diagonal is 24 metre and perimeter 52 metre.

Example 14. The lengths of two parallel sides of a trapezium are 91 cm and 51 cm and the lengths of two other sides are 37 cm and 13 cm respectively. Determine the area of the trapezium.

Solution:

 

 

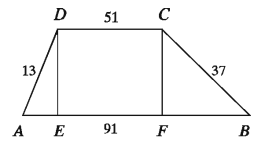
Let, in trapezium ABCD; AB = 91cm CD = 51cm D

Let us draw the perpendiculars DF and CF on AB from D and C respectively.

∴CDEF is a rectangle.

∴ EF = CD = 51cm

Let ,AE=x and DE=CF=h

2. BF = AB – AF = 91 – (AE + EF) = 91 – (x + 51) = 40 – x

From the right-angled triangle ADE we get,

A * E² + D * E ² = A * D² or, x ² + h² = 13² or, x ² + h ² =169…(1)

Again in the-right angled triangle BCF

B * F² + C * F² = B * C² * or , (40 – x)² + h² = 37²

or, 1600 – 80x + x² + h² = 1369

or, 1600 – 80x + 169 = 1369 [From (1)]

or, 1600 + 169 – 1369 = 80x

or ,80x=400

∴x=5

Now putting the value of z in equation (1) we get,

5² + h² = 169or ,h² =169-25=144 therefore h=12

Area of the trapezium ABCD = = 1/2(AB + C (AB+ CD). h

= 1/2 * (91 + 51) * 12 square cm = 71 * 12 square cm = 852 square cm

The required area is 852 square cm.

See more:

• Finite Series
• Heat and temperature