Today is our topic of discussion Theorems about Circles and Triangles .
Theorems about Circles and Triangles
In this section some important theorems about circles and triangles will be presented logically. It is mandatory for the students to know the similarity of two triangles before proving the theorems. Similarity of triangles is discussed thoroughly in Secondary Geometry. For the convenience of the students, we will briefly recapitulate the similarity of triangles.
Equiangularity:
Two polygons having the same number of sides with successive equal angles are said to be equiangular polygons.
Similarity:
Two polygons having the same number of sides are said to be similar if one can establish a one-one correspondence among their vertices such that
1) The corresponding angles are equal and
2) The corresponding sides are proportional.
In this case the two polygons are called similar polygons.
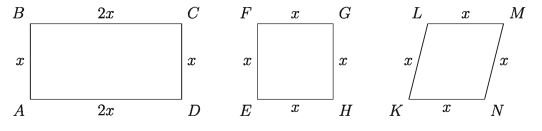
If you take a look at the figure above, you will see that,
1) The rectangular ABCD and square EFGH are equiangular but not similar. All of their corresponding angles are right angle, but their corresponding sides are not proportional.
2) The square EFGH and rhombus KLMN are not similar, since their corresponding sides are proportional because of any successive matching of their vertex but their corresponding angles are not equal.
However, it is not the same in the the case of two triangles. If one condition of the mentioned two regarding the matching of the angles of the vertices of two triangles is true, the other one will be true as well and the two triangles will become similar. It should be mentioned in this regard that,
1) If two triangles are equiangular, each pair of equal angles are called corresponding angles and the sides opposite to the corresponding angles are called corresponding sides.
2) If the three sides of a triangle are proportional to the sides of another triangle, each pair of proportional sides are called corresponding sides, and the angles opposite the corresponding sides are called corresponding angles.
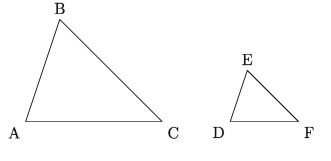
3) In both cases the triangles are described by matching a one-one correspondence among their vertices of the angles. For example, the corresponding angles are ∠A and ∠D, ∠B and ∠E, ∠C and ∠F; the corresponding sides are AB and DE, AC and DF, BC and EF, in case of ΔABC and ΔDEF.
Some theorems about the similarity of the two triangle are briefly described below.
Theorem 6.
If two triangles are equiangular, their corresponding sides are proportional.
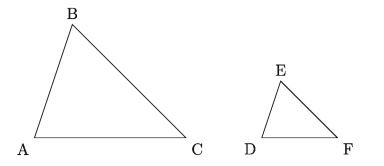
In the figure above, AABC and ADEF equiangular triangles.
Therefore, since ∠A = ∠D, ∠B = ∠E and ∠C = ∠F then AB /DE= AC /DF= BC /EF’
That is, the corresponding sides will be proportional.
Corollary 1. if two triangles are equiangular, they will be similar.
Remarks: If the two angles of one triangle are equal to the two angles of the other, the two triangles are equiangular, hence similar. This is because, the sum of the three angles of any triangle is two right angles.
Theorem 7.
If the sides of the two triangles are proportional, the opposite angles of the corresponding sides are mutually equal.
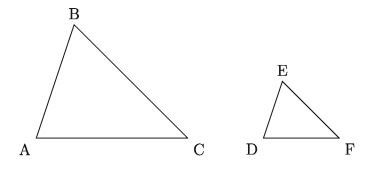
In the figure above, ΔABC and ΔDEF are such that their corresponding sides are proportional i.e., as AB /DE =AC/ DC = DE DF EF’ ZA = ZD, ZB = LE and ZC = ZF. the angles are mutually equal.
Therefore, Theorem 6 is called the converse proposition of the theorem Theorem 7. Theorem 8. If one angle of one triangle is equal to an angle of another triangle and the side adjoining the equal angles are proportional, the two triangles will be similar.
In the figure below, AABC and ADEF are such that A = <D and the sides AB, AC and DE, DF adjoining the equal angles are proportional i.e., as AABC and ADEF are similar. AB AC DE DF’
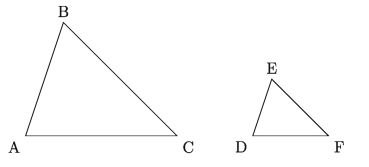
Theorem 9.
The ratio of the areas of the two similar triangles is equal to the ratio of the areas of the squares drawn on their two corresponding sides. In the figure below AABC and ADEF are similar triangles. BC and EF are the corresponding sides of the two triangles. In this condition, the ratio of the two triangles is equal to the ratio of the squares drawn on the two sides BC and ΔΑΒΟ BC2 .Therefore, ADEF EF2 Similarly if AB and DE and AC and DF are the corresponding sides of two triangles, ΔΑΒΟ AB2 AC2 = ADEF DE2 DF2

2 thoughts on “Theorems about Circles and Triangles”