Today is our topic of discussion Geometric Constructions exercises – 4 .
Geometric Constructions exercises – 4
1. If ∠x = 60°, what is the measurement of the half of the supplementary angle of ∠x ?
1) 30°
2) 60°
3) 120°
4) 180°
2. 3.5 cm., 4.5 cm. and 5.5 cm. are the radius of the three circles that touches each other externally, then what is the perimeter of the triangle formed by the the three centres of the circles?
1) 54
2) 40.5
3) 27
4) 13
Answer the questions 3 and 4 in according to the following figure-
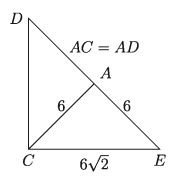
3. What is the value of ∠ADC?
1) 30°
2) 45°
3) 60°
4) 75°
4. What is the ratio of the area ΔADC and AAEC?
1) 2:1
2) 1:1
3) 1:2
4) 1:√2
5. Two angles and the difference of the lengths of their opposite sides of any triangle are given, draw the triangle.
6. The base, the difference of the angles adjoining the base and the sum of the other two sides are given, draw the triangle.
7. The base, the vertical angle and the sum of the other two angles are given. Draw the triangle.

8. The base, the vertical angle and the difference of the other two angles are given. Draw the triangle.
9. The length of the hypotenuse and the sum of the other two sides of a right angle triangle are given. Draw the triangle.
10. A base adjacent angle, height and the sum of the other two sides of a triangle are given. Draw the triangle.
11. (i) Given the length of the hypotenuse and the difference of the lengths of the other two sides are given. Draw the triangle.
(ii) Three medians of a triangle are given. Draw the triangle.
12. Draw a circle which touches a definite straight line at a definite point and another circle.
1
3. Draw a circle which touches a definite straight line at a definite point and another circle at any point.
14. Draw a circle which touches a given straight line at some point and also touches a given circle at a certain point on it.
15. Draw three circle of such different radius that they touch each other externally.
16. P is any point on a chord AB of a circle with the centre O. Draw a chord CD through P such that CP² = AP PB.
17. In an isosceles triangle, the base has the length 5 cm. and the equal sides have he length 6 cm.
1) Draw the triangle.
2) Draw the circumcircle of the triangle and measure its radius.
3) Draw a circle which touches a point P of the circle whose radius is equal to the circumradius of the previous triangle and which passes through the point Q outside that circle.

18. The radius of a circle is 3 cm. with the centre O and T is a point at a distance of 5 cm. from O.
1) Construct the figure in accordance with the above information.
2) Draw two tangents of the circle from T.(Construction and description is must)
3) Determine the sum of the length of the two tangents by using pythagorus theorem.
See more:

4 thoughts on “Geometric Constructions exercises – 4”