Today is our topic of discussion Infinite Series .
Infinite Series

Sequence and finite series are discussed in detail in the General Mathematics Book of Class IX-X. There is a direct relationship between sequence and infinite series. Infinite series can be obtained after assigning plus signs before the terms of a sequence. Infinite series will be discussed in this chapter. After completing the chapter, the students will be able to –
- explain the idea of a sequence;
- identify the infinite series;
- explain the condition of existing the sum of an infinite geometric series;
- sum of an infinite geometric series;
- transform a recurring decimal number into an infinite geometric series and express in fraction.
Sequences
In the relationships illustrated below, every natural number n is related to its square n² : that is, the set of square numbers {1, 4, 9, 16, …} is obtained for the set of natural numbers N={1, 2, 3, 4 ,…} under a certain rule. This set of arranged sequence numbers is a sequence. When some numbers are arranged successively under a definite rule such that the relationship between any two successive terms is known, then the set of numbers arranged in this way is called a sequence.

The relationship shown above is called a function and is written as f(n) = n ^ 2 The general term of this sequences is n ^ 2 The number of terms of any sequence is infinite. The way to write the sequence in terms of the general term is \{n ^ 2\} , n = 1,2,3,4,… or, \ n^ 2 \ n = 1 ^ (∞) or just, \{n ^ 2\} . The first number of a sequences is called the first term, the second number of a sequences is called the second term and so on. In the above sequence 1, 4, 9, 16,…, first term = 1, second term = 4, and so on. Four more examples of sequences are given below:
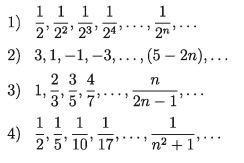
Series
If the terms of a sequences are connected successively by a ‘+’ sign, there a series is formed. As an example, 1+4+9+16+ … is a series. Then again, 1/2+1/4 +1/8 +1/16 +…… is another series. The ratio between two successive terms 2 4 8 16 of this series is the same. This type of series is called Geometric Series. The characteristics of a series depends on the relationship between two consecutive terms of it. For example, in case of Arithmetic Series, the difference between two consecutive terms is constant.
Depending on the number of terms, series can be divided into two classes: 1) Finite series 2) Infinite series. Finite series are discussed in the General Mathematics Book of Class IX-X. Infinite series will be discussed here.
See more:

2 thoughts on “Infinite Series”