Today our topic of discussion is Area of regular polygon.
Area of regular polygon

Area of regular polygon
The lengths of all sides of a regular polygon are equal. Again, the angles are also equal. Regular polygon with n sides produces n isosceles triangles by adding centre to the vertices.
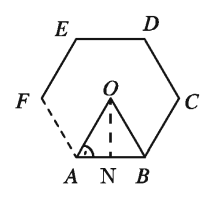
So, area of the regular polygon = n x area of one triangular region ABCDEF is a regular polygon whose centre is O
∴It has n sides and the length of each side is a.
We join O, A; and O, B.
Let height of ΔAOB , ON = h and ∠OAB = θ
The angle produced at each of the vertices of regular
polygon = 2θ
∴ Total angle produced by n number of vertices in the polygon = 2θn
Angle produced in the polygon at the centre = 4 right angles.
∴The sum of angles of number of triangles (2theta*n + 4) right angles.
∴Sum of 3 angles of ΔOAB = 2 right angles.
Summation of the angles of n numbers of triangles = 2n right angles. ln + 4 right angles = 2n right angles.
or, 2θn = (2n – 4) right angles.
or, θ= (2n – 4)/(2n) right angles.
or,θ= (1 – 2/n) * 90 °
θ= 90 °- (180 °)/n
Here, tanθ= (ON)/(AN) = h/(a/2) = (2h)/a
h = a/2 * tanθ
Area of ΔOAB = 1/2 * ah
= 1/2 * a * a/2tanθ
= (a²)/4 * tan(90 °- (180 °)/n)
180° cot- [ tan(90° A) cotA]
. The require area of a regular polygon having n sides = (n * a²)/4 * cot((180 °)/n)
Example 15. If the length of each side of a regular pentagon is 4 cm, determine its area.
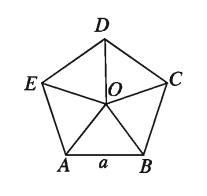
Solution: Let, length of each side of a regular pentagon is a = 4 cm and number of sides n = 5
We know, area of a regular polygon = (n * a ²)/4 * cot((180 °)/n)
∴Area of the pentagon = (5 * 4²)/4 * cot((180 °)/5) square cm
=20 x cot36° square em = 20 * 1.376 square cm (using calculator)
= 27.528 square cm (approx.) Required area 27.528 square cm ( approx .)
Example 16. The distance of the centre to the vertex of a regular hexagon is 4 metre. Determine its area.
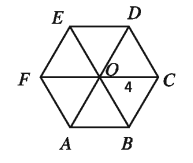
Solution: Let, ABCDEF is a regular hexagon whose centre is 0, 0 is joined to each of the vertex and thus 6 triangles of equal area are formed.
therefore ∠COD = (360°)/6 = 60°
Let the vertex is a metre.
∴ area of ΔCOD = 1/2 * aa * sin 60 °
= √3/4 * 4² square metre = 4√3 =73.74°square metre
Area of the regular hexagon = 6x area of ACOD
= 6 * 4√3 square metre = 24√3 square metre
The required area in 24√3 square metre.
Example 17. According to the given figure
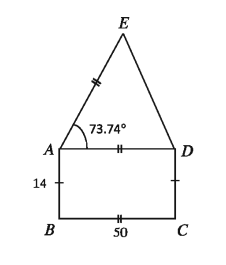
1) Find length of the diagonal of the rectangle.-
2) Find the integer value of its area.
3) Find the perimeter of the isosceles triangle.
Solution:
1) As per the given figure, the area is divided into rectangle ABCD and isosceles ΔADE. Length of diagonal of rectangle ABCD = √(50² + 14²) m =51.92 cm
(approx.)
2) Area of rectangle ABCD = 50 x 14 square cm = 700 square cm Area of ΔADE= 1 2 AD* AE* sin ∠DAE = 1/2 * 50 * 50sin 73.74 deg square cm = 24 * 50 *( cm = 1200
Total area = (700+1200) square cm = 1900 square cm
3) Let, in ∠ADE, AD = AE = 50cm = a, DE = b
∴Area of the isosceles triangle ADE = b/4 * √(4a² – b²)
As per the question, b/4 * √(4a² – b²) = 1200
b * √(4 * (50)² – b²) = 4800
or, b² * (10000 – b²) = 23040000 [by squaring]
or, 10000b² – b 4 = 23040000
or, b4 – 10000b² + 23040000 = 0
or, b4– 6400b² – 3600b² + 2304000 = 0
or, (b² – 6400)(b² – 3600) = 0
∴ b² – 6400 = 0
or, b ² – 3600 = 0
or, b²= 6400 or b² = 3600
∴ b = 80 or b = 60
If b = 80 then 1/2 * ADDE * sin ∠ADE=1200
or 1/2 * 50 * 80 * sin ∠ADE=1200
or, sin ∠ADE = 0.6
∴ ∠ ADE = 36.87 deg (approx.)
Sum of three angles of triangle ADE = 73.74 °+ 36.87 °+ 36.87 °= 147.48 °But sum of three angles of any triangle = 180 °, b≠80
If b = then 60, 1/2 * AD.DE * sin ∠ADE=1200
or 1/2 * 50 * 60 * sin ∠ADE=1200
or, sin ∠ADE = 0.8
∠ADE = 53.13 °(approx.)
Sum of three angles of ΔADE = 73.74 °+ 53.13 °+ 53.13 °= 180 °, therefore b=60
∴The perimeter of the triangle (50 + 50 + 60) cm = 160cm
See more:
