Today our topic of discussion is Circle of Mathematics.
Circle of Mathematics

Circle
We have already known that a circle is a geometrical figure in a plane consisting of points equidistant from a fixed point. Different concepts related to circles like centre, diameter, radius, chord etc have been discussed in previous class. In this chapter, the propositions related to arcs and tangents of a circle in the plane will be discussed.
At the end of the chapter, the students will be able to-
‣ explain arcs, angle at the centre, angle in the circle, quadrilaterals inscribed in the cirlce
‣ prove theorems related to circle
‣ apply of the theorems to solve many problems related to circle
‣ state constructions related to circle.
Circle
A circle is a geometrical figure in a plane whose points are equidistant from a fixed point. The fixed point is the centre of the circle. The closed path traced by a point that keeps it distance from the fixed centre is a circle. The distance from the centre is the radius of the circle.
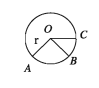
Let, O be a fixed point in a plane and r be a fixed measurement. The set of points which are at a distance r from O is the circle with centre O and radius r. In the figure, O is the centre of the circle and A, B and C are three points on the circle. Each of OA, OB and OC is a radius of the circle.
Some coplanar points are called concylcic if a circle passes through these points, i.e. there is a circle on which all these points lie. In the above figure, the points A, B and C are concyclic.
Interior and Exterior of a Circle
If O is the centre of a circle and r is its radius, the set of all points on the plane whose distances from O are less than r is called the interior region of the circle and the set of all points on the plane whose distances from O are greater than r is called the exterior region of the circle. The line segment joining two points of a circle lies inside the circle.

The line segment drawn from an interior point to an exterior point of a circle intersects a circle at one and only one point. In the figure, P is the interior point and Q is the exterior point of the circle. The line segment PQ intersects the circle at R only.
Chord and diameter of a circle
The line segment connecting two different points of a circle is a chord of the circle. If the chord passes through the centre, it is known as diameter. That is, any chord forwarding to the centre of the circle is diameter. In the figure, AB and AC are two chords and O is the centre of the circle.

The chord AC is a diameter, since it passes through the centre. OA and OC are two radii of the circle. Therefore, the centre of a circle is the midpoint of any diameter. The length of a diameter is 2r, where r is the radius of the circle.
Theorem 17. The line segment drawn from the centre of a circle to bisect a chord other than diameter is perpendicular to the chord.
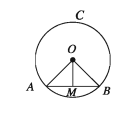
Let AB be a chord (other than diameter) of a circle ABC with center O and M be the midpoint of the chord. Join O, M. It is to be proved that the line segment OM is perpendicular to the chord AB. Drawing: Join O, A and O, B.
Proof:
Step 1. In ∠OAM and ∠OBM,
AM = BM [ M is the mid point of AB]
OA = OB
and OM = OM [common side]
Therefore, ΔΟΑΜ = ΔΟΒΜ [SSS theorem]
∴∠OMA = ∠OMB
Step 2. Since the two angles together make a straight angle and are equal.
Therefore, ∠OMA =∠OMB = 1 right angle.
Therefore, OM ⊥ AB. (Proved)
Corollary 1. The perpendicular bisector of any chord passes through the centre of the circle.
Corollary 2. A straight line can not intersect a circle in more
Work:
The theorem 17 opposite of the theorem states as follows: the perpendicular from the centre of a circle to a chord bisects the chord. Prove the theorem.
Theorem 18. All equal chords of a circle are equidistant from the centre.
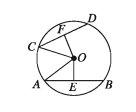
Let AB and CD be two equal chords of a circle with centre O. It is to be proved that the chords AB and CD are equidistant from the centre O.
Drawing: Draw from O the perpendiculars OE and OF to the chords AB and CD respectively. Join O, A and O, C.
Proof:
Step 1. OE perp AB and OF perp CD
Therefore, AE = BE and CF = DF [ centre bisects the chord ]
AE = 1/2 * AB and CF = 1/2 * CD [ The perpendicular from the ]
Step 2. But AB = CD [supposition]
AE = CF
Step 3. Now in the rig t-angled triangles ΔOAE and Δ OCF and
hypotenuse OA = hypotenuse OC [radius of same circle]
AE = CF [Step 2]
∴ ΔOAE ≅ Δ OCF
OE = OF [RHS theorem]
Step 4. But OE and OF are the distances from 0 to the chords AB and CD respectively.
Therefore, the chords AB and CD are equidistant from the centre of the circle. (Proved)
Theorem 19. Chords equidistant from the centre of a circle are equal.
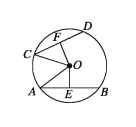
Let AB and CD be two chords of a circle with centre AB and CD respectively. It is to be proved that if.
Drawing: Join O, A and O, C.OE and OF are the perpendiculars from 0 to the chords AB and CD respectively. Then OE and OF represent the distance from centre to the chords.
∴OE = OF, AB = CD
Proof:
Step 1. Since OE perp AB and OF perp CD
Therefore,∠OEA= ∠OFC = 1 right angle.
Step 2. Now in the right angled triangles ΔOAE and ΔOCF
hypotenuse OA = hypotenuse OC [radius of same circle]
And OE = OF [supposition]
∴ ΔOAE ≅ ΔOCF [RHS theorem]
∴ AE = CF
Step 3. AE = 1/2 * AB and CF = 1/2 * CD [ The perpendicular from the centre bisects the chord]
Step 4. Therefore, 1/2 * AB = 1/2 * CD
∴ AB = CD (Proved)
Corollary 3. The diameter is the greatest chord of a circle.
Read more:
