Today our topic of discussion is classification of real numbers.
Classification of Real Numbers

Classification of Real Numbers
Natural Number: 1,2,3,4,… etc are natural numbers or positive whole numbers. 2,3,5,7,…. are primes and 4, 6, 8, 9,….. etc are composite numbers. If GCD (Greatest Common Divisor) of two integers is 1 then they are called mutually primes. For example 6 and 35 are mutually primes.
Integer: All positive and negative fractionless numbers are said to be integers. For example, …, -3, -2, -1,0,1,2,3,… etc are integers.
Fractional Number: Numbers expressible as p/q are said to be factional numbers where q ≠ 0. q ≠ 1 and p are not divisible by q. For example, 1/2, 3/2, – 5/3, 4/6 etc. are simple fractional numbers. In case of a simple fraction p/q if p < q then the fraction is called proper and if p > q then the fraction is termed improper. For example 1/2, 1/3, 2/3, 1/4 etc are proper fractions. 3/2, 4/3, 5/3, 5/4 etc are improper fractions.
Rational Number: Numbers of the form p/q are called rational when p and q 3 are integers and q ≠ 0 . For example, = 3, 11/2 = 5.5 5/3 = 1.666 … etc are rational numbers. Any rational number can be expressed as ratio of two mutually prime numbers. All integers and fractions are rational numbers.
Irrational Number: If a number cannot be expressed in the form p/q where p and q are integers and q ≠ 0 then it is called an irrational number. Root of a natural number not equal to perfect square or its fraction is an irrational number.
For example, √2 =1.414213…, √3 =1.732…, √5/2 =1.118…, etc are irrational numbers. No irrational number can be expressed as ratio of two integers.
Decimal Fractional Number: Rational and irrational numbers when expressed using decimal sign are called decimal fractional number For example, 3 = 3.0, 5/2 = 2.5 10 3 = 3.3333…, √3 = 1.732…, etc are decimal fractional numbers.
If there are finite number of digits after decimal sign, then this is called finite decimal fraction and if there are infinitely many digits, then it is called infinite decimal fractions. For example, 0.52, 3.4152 etc are finite decimal fractions, whereas 4/2 =1.333…, √5 =2.123512367…,etc are infinite decimal fractions.
Again, in case of infinite decimal numbers, if some degits after decimal point are repeated, they are called infinite repeated decimal fractions. If digits are not repeated, they are called infinite decimal numbers without repeatation.
For example, 122/99 = 1.2323 ,..,5.1 dot 6 5 dot 4 etc are infinite repeated decimal fractions and 0.523050056…, 2.12340314… etc are infinite decimal numbers without repeatation.
Real Number: All rational and irrational numbers are called real numbers. For example, the following numbers are real numbers. 0, ±1 , ± 2 ,±3,…
±1/2, ± 3/2 , ± 4/3
√2 √3, √5, √7,***
1.23, 0.415, 1.3333…, 0.62, 4.120345061…
Positive Number: All real numbers bigger than 0 are called positive numbers. For example, 2, 1/2, 3/2 , √2, 0.415, 0.62, 4.120345061…, etc are positive numbers.
Negative Number: All real numbers smaller than 0 are called negative numbers. For example, -2, negative numbers. – 1/2 – 3/2 – √2 −0.415, −0.62, -4.120345061…, etc are negative numbers.
Non-negative Number: All positive numbers including 0 are called nonnegative 1 numbers. For example, 0, 3, 2,0.612, 1.3, 2.120345…, etc are no-negative numbers.
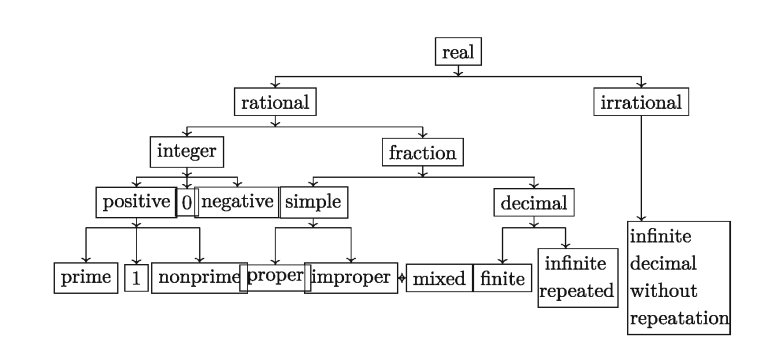
In the following chart we can see classification of real numbers.
Example 1. Find an irrational number between √3 and 4.
Solution: Here, √3 = 1.7320508
Suppose, a and b are two irrational numbers between √3 and 4.
Where a = √3 + 1 and b = √3 + 2
Obviously a and b are both irrational numbers and both are between √3 and 4.
That is, √3 < √3 + 1 < sqrt(3) + 2 < 4... a and b are the two desired irrational numbers.
In fact, we can construct countless number of such irrational numbers.
Basic characteristics of addition and multiplication processes of real numbers:
- If a and b are real numbers, (i) a + b is a real number and (ii) ab is a real number.
- If a and b are real numbers, (i) a + b = b + a and (ii) * ab = ba 3.
- If a, b, c are real numbers, (i) (a + b) + c = a + (b + c) and (ii) (ab) * c = a(bc)
- If a is real number, there are only two real numbers 0 and 1 such that (i) 0 ne1,(ii)a+0=0+a=a and(iii)a*1=1* a=a
- If a is real number, (i) a + (- a) = 0(ii) If a ne0 ,then a * 1/a = 1
- If a, b, c are real numbers, a(b + c) = ab + ac
- If a, b are real numbers, a < b or a = b or a > b
- If a, b, c are real numbers and a < b then a + c < b + c
- If a,b,c are real numbers and a < b then (i) ac < bc whenever c > 0 (ii) ac > bc whenever c < 0.
Proposition: √2 is an irrational number.
Proof: Suppose, √2 is an irrational number.
Then there are two mutually prime numbers p, q > 1,so that √2 = p/q
Or, 2= (p²)/(q²) floor squaring] that is 2q= (p²)/q [ multiplying both sides by q]
Obviously 2q is an integer but (p²)/q is not an integer, because p and q are natural numbers and they are mutually prime and q > 1 .
∴ 2q and (p²)/q cannot be equal, that is 2q≠(p²)/q .
∴ √2 cannot be expressed in the form p/q that is √2 ≠ p/q
∴ √2 is an irrational number.
Remarks: ◊ is used as the end mark of logical proof
Work: Prove that √3 is an irrational number.
Example 2. Prove that when one is added to the product of 4 consecutive natural numbers this becomes a perfect square.
Solution: Let the consecutive integers be x, x + 1 , x + 2 , x + 3
If we add 1 to the product of these 4 integers we get:
x(x + 1)(x + 2)(x + 3) + 1
= x(x + 3)(x + 1)(x + 2) + 1
= (x ² + 3x)(x ² + 3x + 2) + 1
= a(a + 2) + 1 [Assume x ² + 3x =a]
= a ²+ 2a + 1 = (a + 1) ²
= (x ² + 3x + 1) ²

which is a perfect square. Therefore, when 1 is added to the product of any four consecutive natural numbers, this becomes a perfect square.
Read more:
