Today our topic of discussion is Common tangent.
Common tangent

Common tangent
If a straight line is a tangent to two circles, it is called a common tangent to the two circles. In the adjoining figures, AB is a common tangent to both the circles. In figure (a) and (b), the points of contact are different. In figure (c) and (d), the points of contact are the same. If the two points of contact of the common tangent to two circles are different, the tangent is said to be,
1) direct common tangent if the two centres of the circles lie on the same side of the tangent and
2) transverse common tangent, if the two centres lie on opposite sides of the tangent.
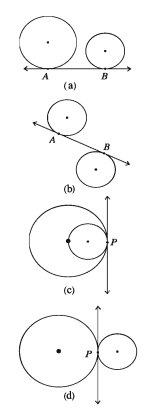
The tangent in figure (a) is a direct common one and in figure (c) it is a transverse common tangent. If a common tangent to a circle touches both the circles at the same point, the two circles are said to touch each other at that point.
In such a case, the two circles are said to have touched internally or externally according to their centres lie on the same side or opposite side of the tangent. In figure (c) the two circles have touched each other internally and in figure (d) externally,
Theorem 25. The tangent drawn at any point of a circle is perpendicular to the radius through the point of contact of the tangent.
Let PT be a tangent at the point. P to the circle with centre O and OP is the radius through the point of contact. It is required to prove that, PT perp OP
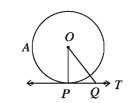
Drawing: Take any point Q on PT and join
Proof: Since PT is a tangent to the circle at the point P, hence every point on PT except P lies outside the circle. Therefore, the point Q is outside of the circle.
∴ OQ is greater than OP that is, OQ > OP and it is true for every point Q on the tangent PT except P.
∴ So, OP is the shortest distance from the centre O to PT.
Therefore, PT perp OP [Among all the line segments drawn from an external point to a straight line, the perpendicular is the shortest] (Proved)
Corollary 8. At any point on a circle, only one tangent can be drawn.
Corollary 9. The perpendicular to a tangent at its point of contact passes through the centre of the circle.
Corollary 10. At any point of the circle the perpendicular to the radius is a tangent to the circle.
Theorem 26. If two tangents are drawn to a circle from an external point, the distances from that point to the points of contact are equal.
Let P be a point outside a circle ABC with centre O and two line segments PA and PB be two tangents to the circle at points A and B. It is required to prove that, PA = PB.

Drawing: Join O, A; O, B and O, P.
Proof:
Step 1. Since PA is a tangent and OA is the radius through the point of tangent, PA perp OA
∴∠PAO = 1 right angle. [ The tangent is perpendicular to the radius through the point of contact of the tangent]
Similarly, ∠PBO = 1 right angle.
∴ triangle PAO and triangle PBO are right-angled triangles.
Step 2. Now in the right angled triangles triangle PAO and triangle PBO
hypotenuse PO = hypotenuse PO and OA = OB [. Radius of the same circle]
ΔPAO ≅ ΔPBO triangle [Hypotenuse-side unanimity of right angled ]
∴PA = PB (Proved)
Remarks:
- If two circles touch each other externally, all the points of one excepting the point of contact will lie outside the other circle.
- If two circles touch each other internally, all the points of the smaller circle excepting the point of contact lie inside the greater circle.
Theorem 27. If two circles touch each other externally, the point of contact of the tangent and the centres are collinear.
Let the two circles with centres at A and B touch each other externally at O. It is required to prove that the points A, O, B are collinear.
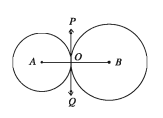
Drawing: Since the given circles touch each other
at O,they have a common tangent at the point O. Now draw the common tangent POQ at O and join O, A and O, B.
Proof:
In the circles with the centre A, OA is the radius through the point of contact of the tangent and POQ is the tangent.
Therefore ∠POA = 1 right angle. Similarly, ∠ POB = 1 right angle.
∠POA+ ∠POB = 1 right angle + 1 right angle = 2 right angles
Or, ∠AOB = 2 right angles
i.e. ∠AOB is a straight angle.
∴ A, O, B are collinear. (Proved)
Corollary 11. If two circles touch each other externally, the distance between their centres is equal to the sum of their radii
Corollary 12. If two circles touch each other internally, the distance between their centres is equal to the difference of their radii.
