Today our topic of discussion is Construction of Quadrilaterals.
Construction of Quadrilaterals

Construction of Quadrilaterals
We have seen if three independent data are given, in many cases it is possible to construct a definite triangle. But with four given sides the construction of a definite quadrilateral is not possible. Five independent data are required for construction of a definite quadrilateral. A definite quadrilateral can be constructed if any one of the following combinations of data is known:
- Four sides and an angle
- Four sides and a diagonal
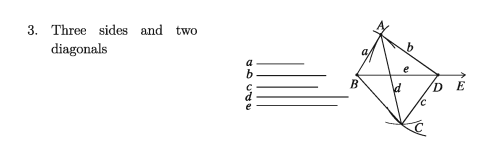
- Three sides and two diagonals
- Three sides and two included angles
- Two sides and three angles.
In class VIII, the construction of quadrilaterals with the above specified data has been discussed. If we closely look at the steps of construction, we see that in some cases it is possible to construct the quadrilaterals directly.
In some cases, the construction is done by constructions of triangles. Since a diagonal divides the quadrilateral into two triangles, when one or two diagonals are included in data, construction of quadrilaterals is possible through construction of triangle.




Sometimes special quadrilaterals can be constructed with fewer data. In such a case, from the properties of quadrilaterals, we can retrieve five necessary data. For example, a parallelogram can be constructed if only the two adjacent sides and the included angle are given.
In this case, only three data are given. Again, a square can be constructed when only one side of the square is given. The four sides of a square are equal and an angle is a right angle; so five data are easily specified.
Construction 4. Two diagonals and an included angle between them of a parallelogram are given. Construct the parallelogram.
Let a and b be the diagonals of a parallelogram and ∠r be an angle included between them. The parallelogram is to be constructed.

Drawing: From any ray AE, cut the line segment AC equal to a. Bisect the line segment AC to find the mid-point O. At O construct the angle ∠AOP equal to ∠x and extend the ray OP to the opposite ray OQ. From the rays OP and OQ cut two line segments OB and OD equal to 1/2 * b Join A, B; A, D; C, B and C, D.
Then, ABCD is the required parallelogram.
Proof: In AAOB and ACOD,
OA = OC = 1/2 * a OB = OD = b [by construction]
and included ∠AOB = included ∠COD [opposite angle]
Therefore, ΔAOB ≅ ΔCOD
So, AB = CD
mp and ∠ABO = ∠CDO: but the two angles are alternate angles.
.. AB and CD are parallel and equal.
Similarly, AD and BC are parallel and equal.
Therefore, ABCD is a parallelogram with diagonals
AC = AO + OC = 1/2 * a + 1/2 * a = a and BD = BO + OD = 1/2 * b + 1/2 * b = b the angle included between the diagonals is ∠AOB = ∠x
Therefore, ABCD is the required parallelogram.
Construction 5. Two diagonals and a side of a parallelogram are given. Construct the parallelogram.
Let a and b be the diagonals and c be a side of the parallelogram. The parallelogram is to be constructed.

Drawing: Bisect the diagonals a and b into two equal parts. From any ray AX, cut the line segment AB equal to c. With centre at A and B draw two ares with radius a/2 and b/2 respectively on the same side of AB. Let the arcs intersect at O. Join A, O and B, O_{i} Extend AO to AE and BO to BF. Now cut a/2 = OC from OE and from OF. Join A, D; D, C and B, C.
b/2 = OD Therefore, ABCD is the required parallelogram.
Proof: In ΔAOB and ΔCOD,
OA = OC = a/2 OB = OD = b/2 and included ∠AOB = included ∠COD [by construction]
[opposite angle]
ΔAOB ≅ ΔCOD
.. AB = CD and ∠ABO = ∠ODC; but the angles are alternate angles.
AB and CD are parallel and equal.
Similarly, AD and BC are parallel and equal.
Therefore, ABCD is the required parallelogram.
Example 3. The parallel sides and two angles included with the larger side of a trapezium are given. Construct the trapezium.
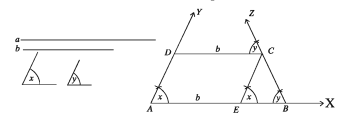
Let a and b be the parallel sides of a trapezium where a > b and Zr and angle y be two angles included with the side a. The trapezium is to be constructed.
Drawing: From any ray AX, cut the line segment AB = a At A of the line. segment AB, construct the angle ∠BAY equal to ∠x at B, construct the angle
∠ABZ equal to ∠y .
Now from the line segment AB, cut a line segment AE=b. AtE . construct EC ||AY which cuts BZ at C. Now construct CD || BA. The line segment CD intersects the ray AY at D. Then, ABCD is the required trapezium.
Proof: By construction, AE || CD and AD ||EC.
Therefore AECD is a parallelogram and CD = AE = b
Now in the quadrilateral ABCD, AB = a, CD = b
AB || CD and Lx, ∠ABC = ∠y [by construction]
∠BAD =
Therefore, ABCD is the required trapezium.
Work: The perimeter and an angle of a rhombus are given. Construct the rhombus.
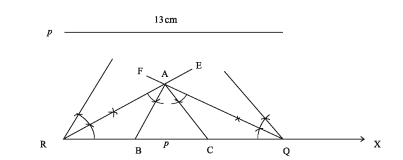
Example 4. In the triangle ABC, ∠B = 60 ° ∠C = 45 °and perimeter p =13cm.
1) Construct ∠B and ∠C with scale and compass.

2) Construct the triangle. (Construction and description of construction are must)
3) Construct a rhombus whose length is equal to p/3 and an angle equal to ∠B (Construction and description of construction is are must)

Solution:
1) Cut RQ = p from any ray RX. Draw ∠B = ∠ERX at the point R and draw C = /FQR at the point. Q. ER and FQ intersect each other at 1 the point A. Now draw∠RAB = ∠B and∠QAC = ∠C at the point A where ∠ERX of the side ER and ∠FQR of the side FQ lic, respectively. The line segment AB and AC intersect at the point B and C of the line RQ.
∴ ABC is the required triangle.
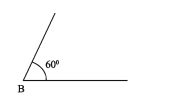
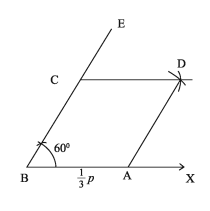
3) Given sides of rhombus is p and an angle is ∠B= 60°. Construct the = rhombus.
Cut BA = 1/3 * p from any ray BX. Draw ∠ABE = overline 60^ at the point B. Take BC = AB from BE. centring the point A and C, draw two arcs of equal radius with 1/3 * p in the interior of ∠ABC The arcs intersects each other at the point D. Join A, D; C, D.
∴ ABCD is the required rhombus.
Read more:
