Construction of Triangles

Today our topic of discussion is Construction of Triangles.

Construction of Triangles

 

 

Practical Geometry

In the previous classes geometrical figures were drawn in proving different propositions and in the exercises. There was no need for precision in drawing these figures. But sometimes precision is necessary in geometrical constructions.

For example, when an architect makes a design of a house or an engineer draws different parts of a machine, high precision of drawing is required. In such geometrical constructions, one makes use of ruler and compasses only.

We have already learnt how to construct triangles and quadrilaterals with the help of ruler and compasses. In this chapter we will discuss the construction of some special triangles and quadrilaterals.

At the end of the chapter, the students will be able to –

‣ explain triangles and quadrilaterals with the help of figures.

‣ construct triangle by using given data.

‣ construct quadrilateral, parallelogram, trapezium by using given data.

Construction of Triangles

Every triangle has three sides and three angles. But, to specify the shape and size of a triangle, all sides and angles need not to be specified. For example, as sum of the three angles of a triangle is two right angles, one can easily find the measurement of the third angle when the measurement of the two angles of the triangle is given.

Again, from the theorems on congruence of triangles it is found that the following combination of three sides and angles are enough to be congruent. That is, a combination of these three parts of a triangle is enough to construct a unique triangle. In class seven we have learnt how to construct triangles from the following data:

 

 

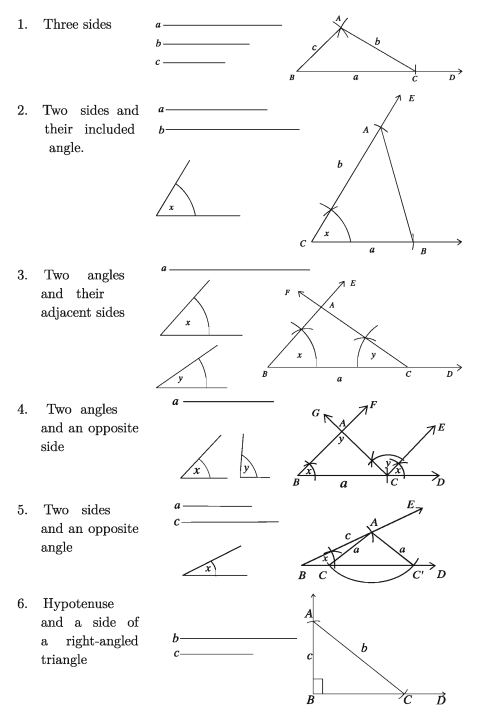
Observe that in each of the cases above, three parts of a triangle have been specified. But any three parts do not necessarily specify a unique triangle. As for example, if three angles are specified, infinite numbers of triangles of different sizes can be drawn with the specified angles (which are known as similar triangles).

 

Sometimes for construction of a triangle three such data are provided by which we can specify the triangle through various drawing. Construction in a few such cases is stated below.

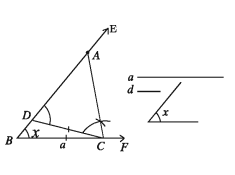
Construction 1. The base, the base adjacent angle and the sum of other two sides of a triangle are given. Construct the triangle.

 

 

Let the base a, a base adjacent angle angle x and the sum s of the other two sides of a triangle ABC be given. It is required to construct it.

Drawing:

1. From any ray BE cut the line segment BC equal to a. At B of the line segment BC, draw an angle ∠CBF = ∠ x
2. Cut a line segment BD equal to s from the ray BF.
3. Join C, D and at C make an angle ∠DCG equal to ∠BDC on the side of DC in which B lies. 
4. Let the ray CG intersect BD at A.

Then, ΔABC is the required triangle,

Proof: In triangle ACD ∠ADC = ∠ACD   [by construction]

∴ AC = AD

Now, in ΔABC, ∠ABC = ∠x. BC = a [by construction]

and BA + AC = BA + AD = BD = s

Therefore, ΔABC is the required triangle.

Alternate Method Let the base a, a base adjacent angle x and the sum s of the other two sides of a triangle be given. It is required to construct the triangle.

Drawing: 

 

 

1. From any ray BE cut the line segment BC equal to a. At B of the line segment BC draw an angle ∠CBF = ∠ x.
2. Cut a line segment BD equal to s from the ray BF.
3. Join C, D and construct the perpendicular bisector PQ of CD.
4. Let the ray PQ intersect BD at A and CD at R. Join A, C.

Then, triangle ABC is the required triangle.

Proof: In triangle ACR and triangle ADR , CR = DR AR = AR and the included ∠ARC = included ∠ARD [right angle]

ΔACR ≅ ΔADR .

∴ AC = AD

Now, In ΔABC ∠ABC = ∠x. BC = a [by construction]

and BA + AC = BA + AD = BD = s Therefore, ΔABC is the required triangle.

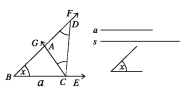
Construction 2. The base of a triangle, an acute angle adjacent the base and the difference between the other two sides are given. Construct the triangle.

 

 

Let the base a_{1} : a base adjacent acute angle angle x and the difference d of the other two sides of a triangle be given. It is required to construct the triangle.

Drawing:

1. From any ray BF cut the line segment BC equal to a. At B of the line segment BC draw an angle angle CBF = ∠x.
2. Cut a line segment BD equal to d from the ray BE.
3. Join C, D and at C make an angle ∠DCA equal to ∠EDC on the side of DC in which E lies

Let the ray CA intersect BE at A. Then, ΔABC is the required triangle.

Proof: By construction, in ΔACD, ∠ACD = ∠ADC

∴ AD = AC

So, the difference of two sides, AB – AC = AB – AD = BD = d

Now, in ΔABC, BC = AB – AC = d and ∠ABC = ∠x

Therefore, ΔABC s the required triangle.

Work:

1) If the given angle is not acute, the above construction is not possible. Why? Explore any way for the construction of the triangle under such circumstances.

2) The base, the base adjacent angle and the difference of the other two sides of a triangle are given. Construct the triangle in an alternate method.

Construction 3. Two angles adjacent to the base and the perimeter of a triangle are given. Construct the triangle.

 

 

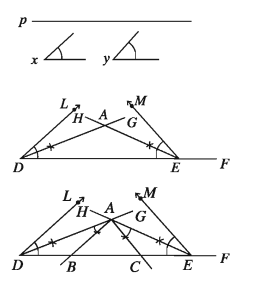
Let the perimeter p and base adjacent angles ∠x and ∠y be given. It is required to construct the triangle.

Drawing:

1. From any ray DF cut the part DE equal to the perimeter p. Make ∠EDL equal to ∠x and ∠DEM equal to∠y on the same side of the line segment DE at D and E.
2. Draw the bisectors DG and EH of the two angles.
3. Let these bisectors DG and EH intersect at a point A. At the point A, draw ∠DAB equal to ∠ADE and ∠EAC equal to ∠AED
4. Let the rays AB and AC intersects DE at the point B and C respectively.

Then, Δ ABC is the required triangle.

Proof: In ΔABD, ∠ADB = ∠DAB  [by construction]

AB = DB

Again, ΔACE, ∠AEC = ∠EAC

CA = CE

Therefore,ΔABC, AB + BC + CA = DB + BC + CE = DE = p

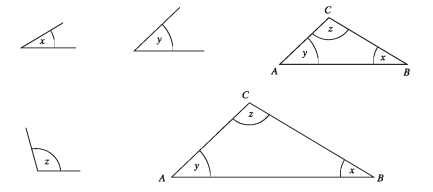
∠ABC = ∠ADB+ ∠DAB= 1/2 ∠x+ 1/2 ∠x= ∠x and ∠ACB = ∠AEC+ ∠EAC= 1/2 ∠y+ 1/2 ∠y= ∠y

Therefore, Δ ABC is the required triangle.

Work: Two acute base adjacent angles and the perimeter of a triangle are given. Construct the triangle in an alternative way.

Example 1. Construct a ΔABC, in which ∠B = 60°. ∠C = 45° and perimeter AB + BC + CA = 11 cm.

 

 

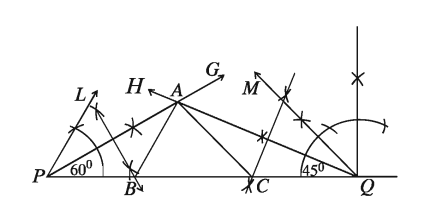
Drawing: Follow the steps below: 

1. Draw a line segment PQ = 11cm .
2. At P, construct an angle of ∠QPL = 60° and at Q, an angle of ∠PQM = 45° on the same side of PQ.
3. Draw the bisectors PG and QH of the two angles. Let the bisectors PG and QH of these angles intersect at A. 
4. Draw perpendicular bisector of the segments PA, QA to intersect PQ at B and C.
5. Join A, B and A, C.

Then, triangle ABC is the required triangle.

Work:

An adjacent side with the right angle and the difference of hypotenuse and the other side of a right-angled triangle are given. Construct the triangle.

Example 2. Base of a triangle a = 3 cm., base adjacent acute angle 45° and the sum of other two sides s = 6cm

1) Express the information of the stem in the picture.

2) Construct the triangle. (Construction and description of construction are must)

3) If the perimeter of a square is 2s, construct the square. (Construction and description of construction are must)

Solution:

1)

 

 

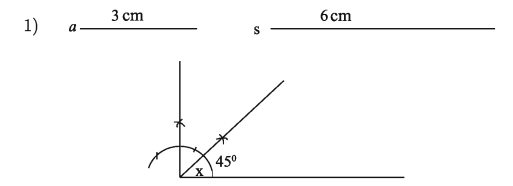
2)

 

Cut AB = a from any ray AX. Draw ∠XAE = x at the point A. Take AD = s from AE. Join B, D. Now draw ∠DBC equal to ∠ADB at the point B. The line segment BC intersects AD at the point C

∴ ABC is the required triangle.

3) Let the perimeter of the square p = 2s We are to draw the square.

 

 

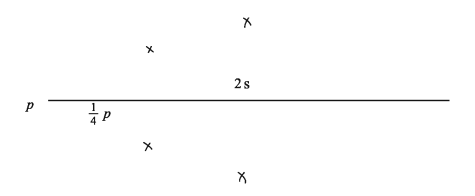
Cut AB = 1/4 * p from any ray AX. Draw AEL AB at the point A. Cut AD = AB from AE. centring the points B and D draw two arcs equal radius of 1/4 * p in the interior of angle BAD . The arcs intersects each other at the point C. Join B, C and C, D.

∴ ABCD is the required square.

Read more:

• Parallel lines
• Principle of calorimetry