Today is our topic of discussion Disjoint Set .
Disjoint Set

If A and B are such sets that A ∩ B = Ø, then A and B are called disjoint sets.
Cartesian Product Set
The Cartesian Product Set of two sets A and B is AxB = {(x, y): x Є A and y Є B}.
Verification of the Two Propositions of the Commutative Law
The shaded area of the following left diagram denotes both A U B and B U A. So in this case, we see that A∪B BUA. On the other hand, the shaded area of the right sided diagram shows both A∩B and BПA. So in this case, it is seen that A∩B = B∩A.
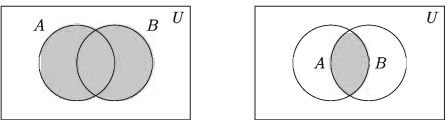
Here the verification shown above is done with the help of Venn Diagram. Now let’s see this with a definite example.
Suppose, A = {1, 2, 4} and B = {2, 3, 5} are two sets.
So, A∪B = {1, 2, 4} U {2, 3, 5} = {1, 2, 3, 4, 5}.
Again, B∪ A = {2, 3, 5} ∪ {1, 2, 4} = {1, 2, 3, 4, 5}.
So in this case, A∪B = B∪A.
On the other hand, A∩B = {1, 2, 4} n (2,3,5)} = {2} and B∩A = {2,3,5} {1, 2, 4} = {2}.
So here, A∩B B∩A.
Verification of the Two Propositions of the Associative Law
The shaded area of the following left diagram denotes both A∪(B∪C) and (A∪B)∪C. So in this case A∪(B∪C) = (AUB)∪C. The shaded area of the right sided diagram shows A∩(BNC) and (An B) nC. So here we can say that (A∩B)∩C= A∩(B∩C).

Here the verification shown above is done with the help of Venn Diagram. Now let’s see this with a definite example.
Suppose, A = {a, b, c, d}, B = {b, c, f} and C = {c, d, g}.
So, BUC= {b, c, f}U {c, d, g} = {b, c, d, f, g} and AU (BUC) = {a, b, c, d} U {b, c, d, f, g} = {a, b, c, d, f, g}.
Again, AUB = {a, b, c, d} U {b, c, f} = {a, b, c, d, f} and (AUB) UC = {a, b, c, d, f}U {c, d, g} = {a, b, c, d, f,g}.
So in this case, (AUB) UC = AU (BUC).
Again, BC= {b, c, f} {c, d, g} = {c} and An (BNC)= {a, b, c, d} {c} = {c}.
Again, AnB = {a, b, c, d} ^ {b, c, f} = {b, c} and (An B) C = {b, c} {c, d, g} = {c}.
So here, An (BNC) = (A∩B)∩c.
Observation:
Each of the operations of union and intersection of sets is distributive with respect to one another.
Proposition 1 (De Morgan’s Law). For any subset A and B of a universal set U,
1) (AUB) A’n B’
2) (ANB) A’U B’
Proof: (The proof of only the first part is shown below. Prove the second one yourself.)
Suppose, E (AUB). So, x AUB.
x A and x B x A’ and x E B’E A’n B’ .. (AUB) CA’B’.
Again, suppose, x E A’n B’. So, x E A’ and x E B’. ⇒ x A and x B x AUBE (AUB) .. A’n B’C (AUB).
Therefore, (AUB) = A’n B’.
Proposition 2. For any subset A and B of a universal set U, A \ B = An B’
Proof: Suppose, Є A \ B. So, x Є A and x & B. ⇒ A and x Є B’⇒ x An B’
.. A\BCAN B’.
Again suppose, xe An B’. So, x E A and E B’.
⇒ x Є A and x 4 B ⇒ x Є A \ B
.. An B’CA\B.
So, A B An B’.
Proposition 3. For any set A, B, C we have,
1) Ax (BNC) = (A x B) n (A x C’)
Forma-2, Higher Mathe, Class-9-10
2) AX (BUC) = (A x B) U (A x C)
Proof: (The proof of only the first part is shown below. Prove the next one yourself.)
According to the definition, Ax (BNC)
= {(x, y): x E A, ye BnC}
= {(x,y): x € A, y € B and y Є C}
= {(x, y): (x, y) = A × B and (x, y) € A× C} =
= {(x, y): (x, y) E (Ax B)n(Ax C)}
Ax (BNC) C (A x B) n (A x C)
Again, (A x B) (A x C)
= {(x, y): (x, y) = Ax B and (x, y) = Ax C}
= {(x, y) : x Є A, y E B and x E A, y € C}
= {(x, y): TEA, y E BN C}
= {(x, y): (x, y) = Ax (BNC)}
.. (Ax B)n (Ax C) CAX (BNC)
So, Ax (BNC) = (A x B) n (A x C).
Some More Propositions of the Method of Sets
1) If A is any set ACA
2) The empty set is the subset of any set A.
3) If A and B are any sets, A = B provided if and only if A C B and B C A.
4) If A CØ, then A = Ø.
5) If ACB and BCC then, AC C.
6) For any set A and B, ABC A and An BC B.
7) For any set A and B, AC AUB and B C AUB. Proof: Only proofs of two propositions are given. Do the others.
see more:

3 thoughts on “Disjoint Set”