Today is our topic of discussion Geometry section exercises – 3.2 .
Geometry section exercises – 3.2
1. In the left sided figure below, which is the orthogonal projection of the line segment AB on XY?
1) AB
2) BC
3) AC
4) XY
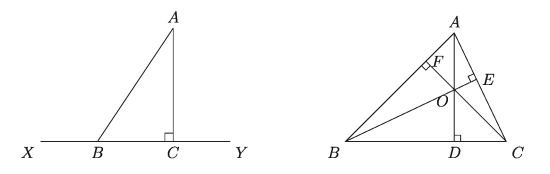
2. In the right sided figure above, which point is the orthocentre of the triangle?
1) D
2) E
3) F
4) O
3. Length of each of the three medians of an equilateral triangle is 3 cm. What is the length of each side?
1) 4.5 cm.
2) 3.46 cm.
3) 4.24 cm.
4) 2.59 cm.

In the figure above, D, E, F are midpoints of BC, AC and AB respectively. In the light of this, answer the questions 4-6:
4. What is the name of the point G?
1) Orthocenter
2) Incenter
3) Centroid
4) Circumcenter
5. What is the name of the circle drawn using the three vertices of ΔABC?
1) Circumcircle
2) Incircle
3) Excircle
4) Nine Point Circle
6. Which statement of the followings is consistent with the Theorem of Apollonius applied to the AABC?
1) AB² + AC² = BC2 3) AB2+ AC² = 2(AG² + GD²)
2) AB² + AC² = 2(AD² + BD²)
4) AB2+ AC² = 2(BD² + CD2)
7. From any point Plying on the circumcircle of the triangle ABC, perpendiculars PD and PE are drawn on BC and CA respectively. If the line segment ED intersects AB at the point O, then prove that, PO is perpendicular to AB, i.e; PO 1 AB
8. ∠C of ΔABC is a right angle. If CD is the perpendicular drawn from the vertex C on the hypotenuse, prove that, CD² = AD.BD
9. AD, BE and CF are the perpendiculars drawn from the vertex of ΔABC to the opposite sides and they intersect at the point O. Prove that, AO OD= BO OE CO. OF
[Hints: ΔBOF and ΔCOE are similar… BO: CO OF: OE.]
10. A semicircle is drawn on the diameter AB. Two of its chords AC and BD intersect at point P. Prove that, AB = AC AP + BD. BP
11. The radius of the circumcircle of an equilateral triangle is 3 cm. Find the length of the side of that triangle.
12. In the isosceles triangle ABC, AD is the perpendicular from vertex A to the base BC. If the circumradius of the triangle is R prove that, AB² = 2R. AD
13. The bisector of the angle ZA of the triangle ABC intersects BC at point D and intersects circumcircle ABC at point E. Show that, AD² = AB AC – BD.DC
14. In the triangle ABC, BE and CF are perpendiculars on the sides AC and AB respectively. Show that, AABC:AAEF = AB2 : AE2
15. In APQR, medians PM, QN and RS intersect at the point O.
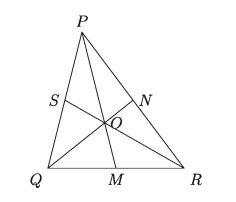
1) What is the name of the point O? In what ratio does point O divide PM?
2) Establish the relation PQ² + PR² = 2(PM² + QM²) from APQR.
3) Show that, the sum of squares of the three sides of APQR is three times the sum of square of distance of the three vertices from point O.
16. In the figure below, S and O are circumcentre and orthocentre of the of the triangle ABC respectively. AP is a median, BC= a, AC = b and AB =c.
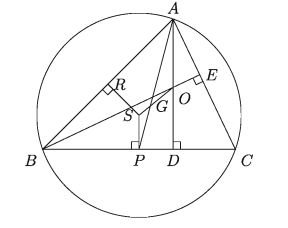
1) Establish a relation between OA and SP.
2) Show that, S, G, O are collinear.
3) If ZC is an acute angle, establish the equation a. CD b. CE

3 thoughts on “Geometry section exercises – 3.2”