Today is our topic of discussion Gradient or slope of a straight line .
Gradient or slope of a straight line
In this part of Coordinate Geometry, at first we shall discuss what Gradient or Slope means and how to determine the Slope or the Gradient of a straight line. By using the concept of the slope how the algebraic form of the straight line appears to be will be discussed. If any straight line passes through two points, the nature of that straight -line and the determination of the equation of that straight line are mainly the subject matter of the discussion.
If two straight lines meet or intersect at any point, determining the coordinates of that intersecting point and triangles formed by three straight-lines denoted by three equations will also be discussed.
Gradient or slope
In the figure beside, let’s consider the straight-line AB. The line passes through the two points A(2, 3) and B(6, 7) . According to the figure, the line produces an angle with the positive side of x axis. The angle is the measurement of the inclination of the straight-line AB with the horizontal x-axis. In Coordinate Geometry, we measure the Gradiant m of the line AB in the following way:

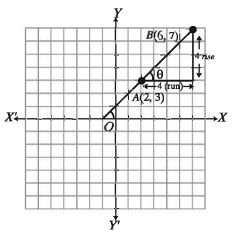
gradient of the line AB, m = 1
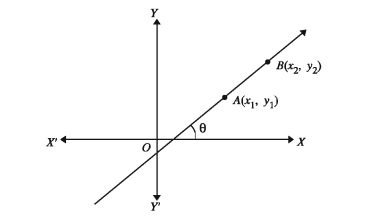
Generally, when a straight-line AB passes through the points A (x1,y1) and B (x²,y²) we express the gradient (m) as

In reality, the relation between the slope m and the angle θ produced by any straight-line with the positive side of x-axis is, m = tanθ . In the figure above, in case of AB, slope of the line is m= 1i .e. , tanθ = 1 or θ = 45° (an acute angle)
See more:

1 thought on “Gradient or slope of a straight line”