Today our topic of discussion is Lines, Angles and Triangles Exercises 6.1.
Line, Ray, Line Segment
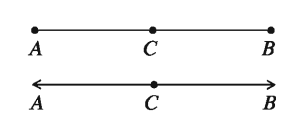
By postulates of plane geometry, every point of a straight line lics in a plane. Let AB be a line in a plane and C be a point on it. The point C is called internal to A and B if the points A, C and B are different points on a line and AC+CB= AB.
The points A, C and B are also called collinear points. The set of points including A and B and all the internal points is known as the line segment AB. The points between A and B are called internal points.
Angle
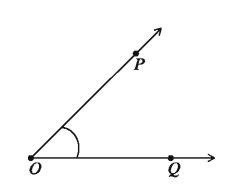
When two rays in a plane meet at a point, an angle is formed. The rays are known as the sides of the angle and the common point as vertex. In the figure, two rays OP and OQ make an angle ∠POQ at their common point O.
O is the vertex of the angle ∠POQ. The set of all points lying in the plane on the Q side of OP and P side of OQ is known as the interior region of the ∠POQ. The set of all points not lying in the interior region or on any side of the angle is called exterior region of the angle.
Straight angle
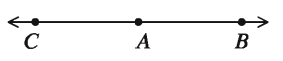
The angle made by two opposite rays at their common end point is a straight angle. In the adjacent figure, a ray AC is drawn from the end point A of the ray AB. Thus the rays AB and AC have formed an ∠BAC at their common point A. ∠BAC is a straight angle. The measurement of a right angle is 2 right angles or 180°.
Adjacent angle
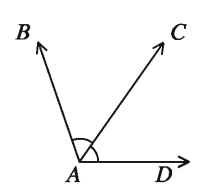
If two angles in a plane have the same vertex, a common side and the angles lie on opposite sides of the common side, each of the two angles is said to be an adjacent angle of the other.
In the adjacent figure, the angles <BAC and ∠CAD have the same vertex A, a common side AC and are on opposite sides of AC. ∠BAC and ∠CAD are adjacent angles.
Perpendicular and Right angle
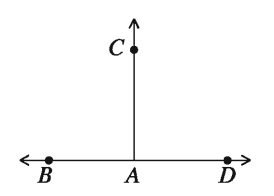
If two adjacent angles are on the same line and equal, then each of the related adjacent angle is a right angle or 90°: The two sides of a right angle are mutually perpendicular. In the adjacent figure two angles∠BAC and ∠DAC are produced at the point A of BD by the ray AC. A is the vertex of these two angles.
AC is the common side of the ∠BAC and ∠DAC. The tow angles lie on the tow sides of the common side AC. If ∠BAC and ∠DAC are equal, then each of the two angles is right angle. The line segments AC and BD are mutually perpendicular.
Acute angle and obtuse angle
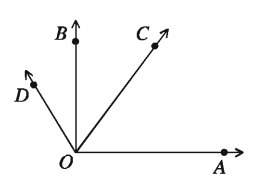
An angle which is less than a right angle is called an acute angle and an angle greater than one right angle but less than two right angles is an obtuse angle. In the figure, ∠AOC is an acute angle and ∠AOD is an obtuse angle. Here∠AOB is a right angle.
Reflex angle
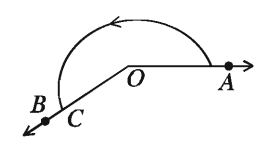
An angle which is greater than two right angles and less than four right angles is called a reflex angle. In the figure, ∠AOC is a reflex angle.
Complementary angle
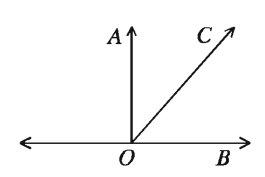
If the sum of two angles is one right angle, the two angles are called complementary angles.
In the adjacent figure, ∠AOB is a right angle. The ray OC is in the inner side of the angle and makes two angles ∠AOC and ∠COB.So taking together the measurement of these two angles is one right angle. The angles ∠AOC and ∠COB are complementary angles.
Supplementary angle
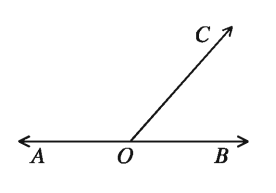
If the sum of two angles is 2 right angles, two angles are called supplementary angles. The point O is an internal point of the line AB. OC is a ray which is different from the ray OA and ray OB. As a result two angles ∠AOC and ∠COB are formed. The measurement of this two angles is equal to the measurement of the straight angle ∠AOB i.e., two right angles. The angles ∠AOC and ∠COB are supplementary angles.
Vertical angle

Two angles are said to be the opposite angles if the sides of one are the opposite rays of the other. In the adjoining figure OA and OB are mutually opposite rays. So are the rays OC and OD. The angles ∠BOD and ∠AOC are a pair of opposite angles. Similarly, ∠BOC and ∠DOA are another pair of opposite angles. Therefore, two intersecting lines produce two pairs of opposite angles.
Theorem 1. The sum of the two adjacent angles which a ray makes with a straight line on its meeting point is equal to two right angles.
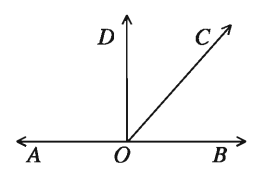
Proof:
Let, the ray OC meets the straight line AB at O. As a result two adjacent angles angle AOC and angle COB are formed. Draw a perpendicular DO on AB. Sum of the adjacent two angles
= ∠AOC + ∠COB= ∠AOD+ ∠DOC+ ∠COB
= ∠AOD+ ∠DOB = 2 right angles.
Theorem 2. When two straight lines intersect, the vertically opposite angles are equal.
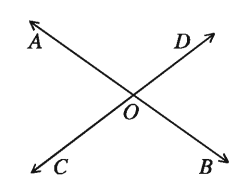
Let AB and CD be two straight lines, which intersect at O. As a result the angles ∠AOC , ∠COB, ∠BOD, ∠AOD are formed at O.
∠AOC = opposite ∠BOD and ∠COB = opposite ∠AOD
Read more:
