Today is our topic of discussion Measurement of Angles .
Measurement of Angles
To measure any angle we use two unit systems :
1) Sexagesimal System and
2) Circular System
Sexagesional System:
In this system right angle is considered as unit of measurement of angle. In this system one degree is one – ninetieth 90 part of a right angle one metre (1° = one degree).
One-minute is one sixtieth 60 part of one degree i.e., ( 1′ = one minute) and that of one-second is one sixtieth 60 part of one minute i.e., 1 ^ prime prime = one second).
That is, 60″ (second) = 1′ (minute)
60′ (minute) = 1 deg (degree)
90° (degree)= 1 right angle
Radian system is necessary to know before circular system.
Radian: In any circle the angle which an arc of the circle whose length is equal to the radius of the circle subtends at the centre, is called one radian.
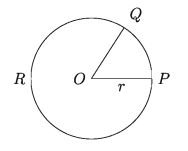
In the figure, the centre of circle PQR is O, radius OP = r and PQ is an arc equal to the radius. Arc PQ produce ∠POQ at the centre O. This measurement of that angle is called radian i.e. ∠POQ is a randian.
Circular System:
In circular system one radian angle is considered as measurement unit of angle. To determine the relation between radian measurement and degree measurement the following proposition need to be known.
Proposition 1. In any two circles the ratios of the circumferences and the respective diameters and equal.
Proof:
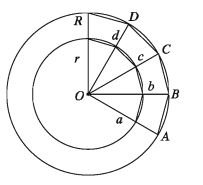
We can assume that the circles have the same centre O and they are concentric. Let p and r denote the circumference and radius of the inner (smaller) circle and P and R denote the circumference and radius of the outer (greater) circle(following figure). We divide the circumference of the outer circle into n equal arcs where (n > 1) . Joining the dividing points with centre the inner circle also divided into n equal parts. Let us join the dividing points of both the circles. We get consequently (outer circle ABCD… and inner circle abcd…) two n sided regular polygons inscribed in the outer and inner circle, respectively.
Now, AOAB and AOab are similar, because, ZAOB and LaOb [common angle] and being isosceles triangles, their other two angles are equal .
(AB/ab) = (OA/Oa) = (OB/Ob) = R/r
Similarly,
(BC/bc) = R/r, (CD)/(cd) = R/r
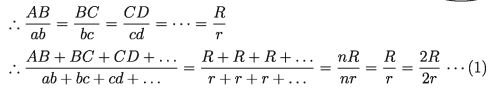
If n is sufficiently large that is letting (n -> ∞) then AB, BC, CD will be very small and seems to be minute arcs of the circle.
Therefore, in this case, AB + BC + CD +……..≈ circumference of the outer circle P and
ab + bc + cd +……… .≈circumference of the inner circle p
from equation (1) we get,
P/p = (2R/2r)
i.e., P/2R= p/ 2r
i.e., circumference of the outer circle/diameter of the outer circle=circumference of the inner circle/diameter of the inner circle
In any circle the circumference bears a constant ratio to its diameter.
By Corollary 1:
Remark: In any circle the circumference bears a constant ratio to its diameter. This constant ratio is denoted by the Greek letter (pi). π is an irrational number and expressing in decimal places it will be non-terminating where, (π = 3.1415926535897932…).
Remark: Generally approximate value of π upto four decimal places is used where = 3.1416. Using computer the value of π has been determined upto millions and millions of digit in decimal place. As we use approximate value of π, answer must be approximated. That is why it is required to write ‘approx’ beside the answer. Approximate value of = 3.1416 will be used as no direction is mentioned.
Corollary 2. The circumference of any circle of radius r is equal to 2πг.
Circumference Diameter П
Proof:
By Corollary 1 we know,
Circumference/Diameter=π
or, Circumference = π Diameter
=π × 2r [Diameter = 2r] = 2πг
Circumference of any circle of radius r is 2″r.
Proposition 3. The centred angle produced by any arc of a circle is proportional to its arc.
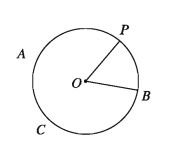
Proof:
OA intersect the circumference at A.
Arc AB one-fourth of the circumference =1/4×2πr/2
And arc PB =radius r [ZPOB = 1 radian]
From corollary 3,
∠POB/AOB= ArcPB /ArcAB
∠POB =ArcPB/ArcAB × ∠AOB = r/πr/2×1 [ Radius OA is perpendicular
to OB]
=2/π right angle.
As the right angle and are constant, ∠POB is a constant angle.
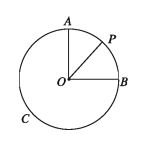
Let O be the centre and OB is radius of the circle ABC. P is another point on the circle. So BP is an arc and POB is the centred angle of the circle. So centred ∠POB is proportional to arc BP. i.e. centred ∠POB xx arc BP.

1 thought on “Measurement of Angles”