Naming of sides of a right-angled triangle

Today our topic of discussion is Naming of sides of a right-angled triangle.

Naming of sides of a right-angled triangle

 

 

Naming of sides of a right-angled triangle

We know that, the sides of right-angle triangle are known as hypotenuse, base and height. This is successful for the horizontal position of triangle. Again, the naming of sides is based on the position of one of the two acute angles of right- angled triangle. As for example:

1. (hypotenuse)’, the side of a right-angled triangle, which is the opposite side of the right angle.
2. (opposite side)’, which is the direct opposite side of a given angle,
3. (adjacent side)’, which is a line segment constituting the given angle.

 

 

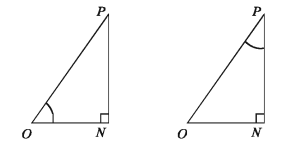
For the angle ∠PON, OP is the hypotenuse, ON is the adjacent side and PN is the opposite side. For the angle∠OPN, OP is the hypotenuse, PN is the adjacent side and ON is the opposite side.

In the geometric figure, the capital letters are used to indicate the vertices and small letters are used to indicate the sides of a triangle. We often use the Greek letters to indicate angle. Widely used six letters of Greek alphabet are:

 

 

Greek letter are used in geometry and trigonometry through all the great mathematician of ancient Greek.

Example 1. Indicate the hypotenuse, the adjacent side and the opposite side for the angle 0.

Solution:

 

 

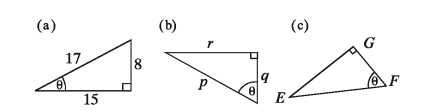
1) Hypotenuse 17 units

 opposite side 8 units

 adjacent side 15 units

 2) Hypotenuse p

 opposite side r

 adjacent side q

 3) Hypotenuse EF

 opposite side EG

 adjacent side FG 

Example 2. Find the lengths of hypotenuse, the adjacent side and the opposite side for the angles a and B.

Solution:

 

 

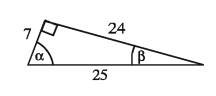
1) For a angle

hypotenuse 25

units adjacent side 7 units

opposite side 24 units

2) For 8 angle

hypotenuse 25 units

adjacent side 24 units

opposite side 7 units

 

 

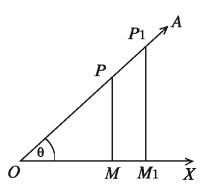
Let ∠XOA is an acute angle. We take a point P on the side OA. We draw a perpendicular PM from P to OX. As a result, a right-angled ΔPOM is formed. The three ratios of the sides PM, OM and OP of ΔPOM do not depend on the position of the point P on the side OA. If we draw the perpendiculars PM and ΔP1Om1 from two points P and P1 to the side OX, two similar triangles ΔPOM and ΔP1Om1 are formed.

Now, ΔPOM and ΔP1Om1 are being similar,

 

 

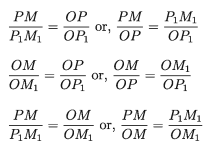
That is, each of these ratios is constant. These ratios are called trigonometric ratios.

See more:

• Common tangent
• Principle of calorimetry