Today our topic of discussion is Parallel lines.
Parallel lines
Parallel lines
Alternate angles, corresponding angles and interior angles of the traversal.

In the figure, two straight lines AB and CD are cut by a straight line EF at P and Q. The straight line EF is a traversal of AB and CD. The traversal has made eight angles ∠1 , ∠2 , ∠3 , ∠24, ∠ 5 , ∠6 , ∠7 , ∠28 with the lines AB and CD. Among the angles
1) ∠1 and ∠5 , ∠2 and ∠6 . ∠3 and ∠7 , ∠4 and ∠8 are corresponding angles.
2) ∠3 and ∠6 . ∠4 and ∠5 are alternate angles. .
3) ∠4 , ∠6 are interior angles on the right
4) ∠3 , ∠5 are interior angles on the left.
In a plane two straight lines may intersect or they are parallel. The lines intersect if there exists a point which is common to both lines. Otherwise, the lines are parallel. Note that two different straight lines may at most have only one point in common.
The parallelism of two straight lines in a plane may be defined in three different ways:
1) The two straight lines never intersect each other (even if extended to infinity).
2) Every point on one line lies at equal smallest distance from the other.
3) The corresponding angles made by a transversal of the pair of lines are equal.
According to definition (a) in a plane two straight lines are parallel, if they do not intersect each other. Two line segments taken as parts of the parallel lines are also parallel.
According to definition (b) the perpendicular distance of any point of one of the parallel lines from the other is always equal. Perpendicular distance is the length of the perpendicular from any point on one of the lines to the other.
Conversely, if the perpendicular distances of two points on any of the lines to the other are equal, the lines are parallel. This perpendicular distance is known as the distance of the parallel lines.
The definition (c) is equivalent to the fifth postulate of Euclid. This definition is more useful in geometric proof and constructions.
Observe that, through a point not on a line, a unique line parallel to it can be drawn.
Theorem 3. When a transversal cuts two parallel straight lines,
1) the pair of corresponding angles are equal.
2) the pair of alternate angles are equal.
3) that pair of interior angles on the same side of the transversal are supplementary.
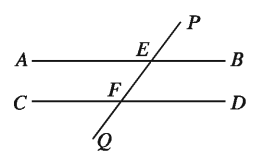
In the figure, AB || CD and the traversal PQ intersects them at E and F respectively.
Therefore,
1) ∠PEB = corresponding ∠EFD [by definition]
2) ∠AEF alternate ∠EFD
3) ∠BEF+∠EFD= 2 right angles
Work:
Using alternate definitions of parallel lines prove the theorems related to parallel straight lines.

Theorem 4. When a transversal cuts two straight lines, such that
1) pairs of corresponding angles are equal, or
2) pairs of alternate angles are equal, or
3) pairs of interior angles on the same side of the transversal are equal to the sum of two right angles, then those two straight lines will be parallel.
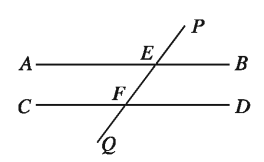
In the figure the line PQ intersects the straight lines AB and CD at E and F respectively and
1) ∠PEB corresponding∠EFD or,
2)∠AEF = alternate ∠EFD or,
3) ∠BEF+∠EFD = 2 right angles Therefore, the straight lines AB and CD are parallel.
Corollary 1. The lines which are parallel to a given line are parallel to each other.
Read more:
