Today is our topic of discussion Partial Sum of Infinite Series .
Partial Sum of Infinite Series

Let u₁+u2+u3 + …….. + Un +… be an infinite series. Then its:
1st partial sum is S₁ = u₁
2nd partial sum is S₂ = u₁ + u₂
3rd partial sum is S3=u1+u2+uз
The n-th partial sum is S₁ = u1+ Uz + Uz + … + Un
That is, the n-th partial sum of an infinite series is the sum of the first n number of terms of the series, where n Є N.
a + ar + axr ^ 2 + axr ^ 3 +… is a geometric series. Its first term is a and common ratio is r.
Therefore, the n-th term of the series = a * r ^ (n – 1) where n in N
Now, if r ne1 then the partial sum of this series upto n – th term is
S n = a + ar + axr ^ 2 + a x r ^ 3 +…+ar^ n-1
We observe:
1) In the case of |r| < 1 that is – 1 < r < 1 , if the value of n increases (that is, when n -> ∞ ) then the value of |r ^ n| decreases. Thus making n sufficiently large, the value can be decreased indefinitely, that is, |r ^ n| approaches 0. So, the limiting value of [r” becomes 0.
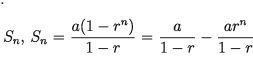
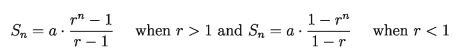
2) In the case of |r| > 1 , that is r > 1 or r < – 1 , if the value of n increases then the value of |r ^ n| increases and making n sufficiently large the value of |r ^ n| can be increased indefinitely. From this it is clear that there does not exist a finite numbers S which can be considered as the limiting value of S_{n}
So, in this case, sum of the infinite series does not exist.
3) If r = – 1 then the limiting value of S_{n} cannot be found. Because, if n is even then (- 1) ^ n = 1 and if n is odd, then (- 1) ^ n = – 1 . In this case the series will be, a – a + a – a + a – a+…
So, sum of this infinite series does not exist.
4) In case of r = 1, limiting value of S, cannot be found as well. Because, in that case the series will be a + a + a + a + … (n numbered). That means, Sn = na which can be increased with the increasing of n.
So, sum of this infinite series does not exist.
See more:

3 thoughts on “Partial Sum of Infinite Series”