Today is our topic of discussion Probability exercises – 14.
Probability exercises – 14
1. Which is the probability of getting 3 in a throw of a dice?
1) 1/6
2) 1/3
3) 2/3
4) 1/2
Answer questions 2 and 3 based on the information given below:
A ball is drawn at random from a bag containing 12 blue, 16 white and 20 black balls.
2. What is the probability that the ball is blue?
1) 1/16
2) 1/12
3) 1/8
4) 1/4
3. What is the probability that the ball is not white?
1) 1/3
2) 2/3
3) 1/16
4) 1/48
Answer questions 4 and 5 based on following information:
A coin is tossed thrice.
4. What is the probability of getting a head more number of times than getting a tail?
1) 1/6
2) 1/3
3) 1/2
4) 2/3
5. What is the probability of getting T zero number of times?
1) 0
2) 1/2
3) 1
4) 1/8
6. In the case of throwing two coins-
(i) Probability of getting at most one H = 0.75
(ii) Probability of getting at least one H = 0.75
(iii) HH is a sample point.
Which one of the following is correct?
1) i, ii
2) i, iii
3) ii, iii
4) i, ii, iii
7. Thirty tickets are numbered serially form 1 to 30. The tickets are mixed thoroughly and one ticket is drawn at random. Find the probability of the serial number of the ticket being
1) an even number
2) divisible by 4
3) less than 4
4) greater than 22.
8. In a certain lottery 570 tickets have been sold. Rahim has bought 15 tickets. The tickets are mixed together thoroughly and one ticket is drawn at random for the first price. What is the probability of Rahim getting the first prize?
9. What is the probability of getting an even number or a number divisible by 3 in a single throw of a dice?
10. According to the report of a health centre, 155 babies were born who were underweight, 386 babies were born with normal weight and 98 babies were born who were overweight. One baby is selected at random from these babies. What is the probability that the baby was overweight?
11. The employees employed in a factory can be classified based on the types of work they perform, as mentioned below:
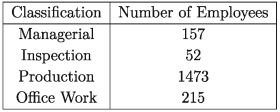
If a person is selected randomly, then what is the probablity of the person being-
1) involved in management duty?
2) involved in managerial or production duty?
3) not involved in production duty?
12. Out of 2000 newly licensed drivers. the following number of drivers violate the traffic rules in a single year.
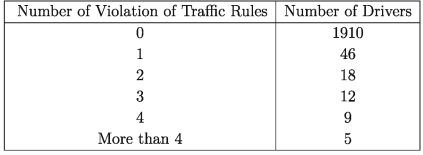
1) Out of these 2000 drivers, if one driver is chosen at random what is the probability that the driver has violated traffic rules once? 2) What is the probability that the driver has violated traffic rules more than 4 times?
13. Form a probability tree for tossing a coin and throwing a dice successively.
14. Fill up the following table with the help of probability trees:
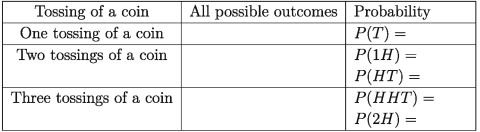
15. The probability that a certain person will travel from Dhaka to Rajshahi 5/9 by train is and that subsequently the person will travel from Rajshahi to 2/7 Dinajpur by bus is Using a probability tree –
1) Find the probability that the person will travel from Dhaka to Rajshahi not by train and then travel to Dinajpur by bus.
2) Find the probability that the person will travel from Dhaka to Rajshahi by train and then travel to Dinajpur not by bus.
16. The probability that a person will travel from Dhaka to Chittagong by train is 2/9 the probability that the person will travel by bus is 3/7 and the 1/9 probability that he will take a flight isThe probability that subsequently 2/5 the person will travel to Cox’s Bazar by bus is and the probability that 3/7 * he will travel by car is Use a probability tree to find the probability that he will travel by train to Chittagong and then by bus to Cox’s Bazar.
17. A two-taka coin is tossed four times. (Denote its side with Water Lily flower by L and the side with the primary school going child by C)
1) If the coin is tossed twice rather than four times, what is the probability of getting a L and that of not getting a C?
2) Draw the probability tree of the possible events and write down the sample space.
3) Show that, if the coin was tossed n times, the total number of possible events is 2″.
18. There are 8 red, 10 white and 7 black marbles in a basket. A marble is chosen randomly.
1) Find all possible outcomes.
2) Find the probability of the marble being (1) Red and (2) Not white.
3) If four marbles are picked up one by one without replacing any one of them, then find the probability of all the marbles being white.

2 thoughts on “Probability exercises – 14”