Today our topic of discussion is Properties of Ratio and Proportion.
Properties of Ratio and Proportion

Ratio, Similarity and Symmetry
For comparing two quantities, their ratios are to be considered. Again, for determining ratios, the two quantities are to be measured in the same units. In algebra we have discussed this in detail.
At the end of this chapter, the students will be able to –
‣ explain geometric ratios.
‣ explain the internal division of a line segment.
‣ verify and prove theorems related to ratios.
‣ verify and prove theorems related to similarity.
‣ explain the concepts of symmetry.
‣ verify line and rotational symmetry of real objects practically.
Properties of Ratio and Proportion
(i) If a : b = x and c: d = x / y it follows that, a : b = c : d
(ii) If a : b = b : a, it follows that, a = b
(iii) If a / b = x / y_{k} it follows that, b / a = y / x (inversendo).
(iv) If a / b = x / y it follows that, a / x = b / y (alternendo).
(v) If a / b = c / d, j follows that, a * d = bc (cross-multiplication)
(vi) If a / b = x / y it follows that, a + b / b = x + y / y (componendo) and a – b/ b = x – y / y (dividendo)
(vii) If a/b = c/d it follows that (a + b)/(a – b) = (c + d)/(c – d) (componendo and dividendo).
Geometric proportions
We have learnt to find the area of a triangular region. Two necessary concepts of ratio are to be formed from this.
- If the heights of two triangles are equal, their bases and areas are proportional.
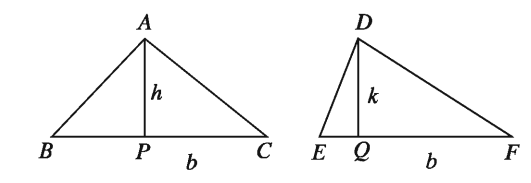
Let the bases of the triangles ABC and DEF be BC = a, EF respectively and the height in both cases be h. = d
Hence, the area of the triangle ABC Therefore, the area of the triangle ABC: area of the triangle DEF = xax h, the area of the ΔDEF
1 =2xaxh xaxh:3 xdxha: d= BC: EF
- If the bases of two triangles are equal, their heights and areas are proportional.

Let the heights of the triangles ABC and DEF be AP = h, DQ = k respectively and the base in both cases be b.
Hence, the area of the triangle ABC = xbxh, and the area of the 2
ΔDEF = xbx k
Therefore, the area of the ΔABC: area of the ΔDEF
= xh: xbxk-h:k- AP: DQ
Theorem 28. A straight line drawn parallel to one side of a triangle intersects the other two sides or those sides produced proportionally.

Special Nomination: In the figure, the straight line DE is parallel to the side BC of the triangle ABC. DE intersects AB and AC (figure-1) or their produced sections (figure-2) at D and E respectively. It is required to prove that
AD / D * B = AE / E * C
Drawing: Join B, E and C, D.
Proof:
Step 1. The heights of AADE and triangle BDE are equal. therefore triangle ADE triangle BDE = (AD)/(DB) proportional] [The bases of the triangles of equal height are
Step 2. The heights of AADE and ADEC are equal
therefore ΔADE ΔDEC = (AE)/(EC)
proportional]
[The bases of the triangles of equal height are
Step 3. But ΔBDE = ΔDEC pair of lines]
[On the same base DE and between same
therefore ΔADE ΔBDE = ΔADE ΔDEC
Step 4. Therefore, (AD)/(DB) = (AE)/(EC)
i .e,AD:DB=AE:EC
Corollary 1. If the line parallel to BC of the triangle ABC intersects the sides AB and AC at D and E respectively, then (AB)/(AD) = A overline C AE and
(AB)/(BD) = (AC)/(CE)
Corollary 2. The line through the mid point of a side of a triangle parallel to another side bisects the third line.
The proposition opposite of theorem 28 is also true. That is if a line segment divides the two sides of a triangle or the line produced proportionally, it is parallel to the third side. Here follows the proof of the theorem.
Theorem 29. If a line segment divides the two sides or their produced sections of a triangle proportionally, it is parallel to the third side.

Special Nomination: In the triangle ABC the line segment DE divides the two sides AB and AC or their produced sections proportionally. That is, AD: DB = AE / E * C It is required to prove that DE and BC are parallel. Drawing: Join B, E and C, D.
Proof:
Step 1. ΔADE ΔBDE = (AD)/(DB) and ΔADE ΔDEC AE EC
[Triangles with equal height]
[Triangles with equal height]
Step 2. But (AD)/(DB) = (AE)/(EC)
[Given]
Step 3. Therefore, ΔADE ΔBDE = ΔADE ΔDEC
ΔBDE = ΔDEC
[ from (i) and (ii)]
Step 4. But ΔBDE and ΔDEC are on the same side of the common base DE. So they lie between a pair of parallel lines.
∴ BC and DE are parallel.
Theorem 30. The internal bisector of an angle of a triangle divides its opposite side in the ratio of the sides constituting to the angle.

Special Nomination: In AABC the line segment AD bisects the internal angle ∠A and intersects the side BC at D. It is required to prove that BD: DC = BA / A * C
Drawing: Draw the line segment CE parallel to DA, so that it intersects the side BA produced at E.
Proof:
Step 1. Since, DA || CE and BE is their transversal [by construction]
∴ angle AEC = angle BAD [corresponding angles] Again, DA | CE and AC is their transversal
∴ ∠ ACE = ∠ CAD [corresponding angles]
Step 2. But ∠ BAD = ∠CAD [supposition]
:. ∠AEC = ∠ACE
Hence, AC = AE [Chapter 6 Theorem 8]
Step 3. Again, since DA || CE Therefore, (BD)/(DC) = (BA)/(AE)
Step 4. But AE = AC (BD)/(DC) = (BA)/(AC)
Theorem 31. If any side of a triangle is divided internally, the line segment from the point of division to the opposite vertex bisects the angle at the vertex.
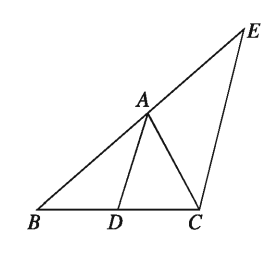
Special Nomination: Let ABC be a triangle and the line segment AD from vertex A divides the side BC at D such that BD / D * C = BA : AC. It is required to prove that AD bisects
∠BAC i.e. ∠BAD = ∠CAD
Drawing: Draw at C the line segment CE parallel to DA, so that it intersects the side BA produced at E.
Proof:
Step 1. For ABCE DA || CE [by construction]
,BA:AE=BD:DC [theorem 28]
Step 2. But BD / D * C = BA AC [supposition]
∴ BA / A * E = BA / A * C
∴ AE = AC [from step 1 and step 2]
∴ ∠ACE = ∠AEC [base angles of isosceles triangle are equal]
Step 3. But ∠AEC = ∠BAD and ∠ACE = ∠ CAD [corresponding angles]
[alternate angles]
Therefore, ∠BAD = ∠CAD [from step 2]
∴ the line segment AD bisects ∠BAC .
See more:
