Trigonometric Ratio Exercises 9.2

Today our topic of discussion is Trigonometric Ratio Exercises 9.2 .

Trigonometric Ratio Exercises 9.2

 

Exercises 9.2

1. If cosθ= 1/2 which one is the value of cotθ ?

1) 1/(√3)

2) 1

3) √3

4) 2

2. If cos²θ- sin² θ= 1/3 what is the value of cos⁴θ- sin⁴ θ?

1) 3

2) 2

3) 1

4) 1/3

3. If cot(θ- 30 °) = 1/(√3) ,sin θ=what ?

1) 1/2

2) 0

3) 1

4) √3/2

4. If tan(3A) = √3 A=what?

1) 45 °

2) 30 °

3) 20

4) 15 °

5. For 0°≤ θ≤ 90 deg what is the maximum value of sin θ=?

1) -1

2) 0

3) 1/2

4) 1

6. ABC is a right-angled triangle whose

 

 

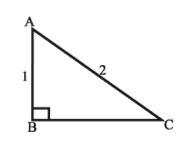
hypotenuse AC = 2, AB = 1

(i) ∠ACB = 30 °

(ii) tan A = √3

(iii) sin(A+C)=0

Which one of the following is correct?

1) i

2) ii

3) i and ii

4) ii and iii

7. ABC is a right-angled triangle whose hypotenuse AC = 2 ,AB = 1

 

 

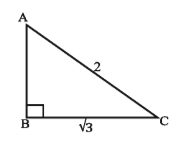
(i) cos A = sin C

(ii) cos A + sec(A) = 5/2

(iii) tan C = 2/√3

Which one of the following is correct?

1) i and ii

2) ii and iii

3) i and iii

4) i, ii and iii

8. (1 – cot²(60 °))/(1 + cot² (60 °))
9. tan 45 °* sin² (60 °) * tan 30 °* tan 60 °
10. (1 – cos²(60 °))/(1 + cos² (60 °)) + sec²(60 °)
11. cos 45 °* cot² (60 °) * co * sec² (30 °)

Show that, (12-17)

12. cos² (30 °) – sin² (30 °) = cos 60 °
13. sin 60 °* cos 30 °+ cos 60 °* sin 30 ° = sin 90 °
14. cos 60 °* cos 30 °+ sin 60 ° * sin 30 °= cos 30 °
15. sin 3A = cos 3A when A = 15 °
16. sin 2A = (2tan A)/(1 + tan² A) when A = 45 °
17. tan 2A = (2tan A)/(1 – tan² A) when A = 30 °
18. 2cos(A + B) = 1 = 2sin(A – B) and A, B are acute angles, show that A = 45 °,B = 15 °
19. If cos(A – B) = 1 , 2sin(A + B)=√3 and A, B are acute angles, determine the values of A and B.
20. Solve: (cos A – sin A)/(cos A + sin A) = (√3 – 1)/(√3 + 1)
21. If A and B are acute angles and cot (A + B) = 1 , cot(A – B) = √(3) determine the values of A and B.
22. Show that, cos 3A = 4cos³ A – 3cos A when A = 30 °
23. Solve: sin θ+ cosθ = 1 when 0° ≤ θ≤ 90 °
24. Solve: cos² θ- sin² θ= 2 – 5cos θ when is an acute angle.
25. Solve: 2sin² θ+ 3cos θ- 3 = 0 0 is an acute angle.
26. Solve: tan² θ- (1 + √3* tan θ+ √3 ) = 0
27. Solve: 3cot² (60°) + 1/4 * cosec² (30°) + 5sin² (45°) – 4cos² (60°)
28. If angle B = 90° . AB = 5cm BC = 12cm of ΔABC

1) Find the length of AC.

2) If angle C = theta . find the value of sin θ+ cos θ3) Using stem show that, sec² A + cosec² A = sec² A * cosec² A

29.

 

 

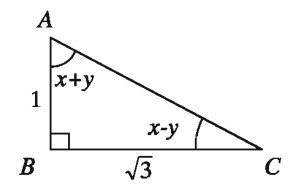
In accordance of the given figure

1) what is the measurement of AC?

2) Find the value of tan A + tan C

3) Find the values of x and y.

30. sin θ= v cos θ= q tan θ= r where is an acute angle.

1) If r = √(3) ^ – 1) find the value of 0.

2) If p + q = √2 prove that θ= 45° 0 3) If 7p²+ 3q ² = 4 show that, tan θ= 1/(√(3))

31. ABC is a right-angled triangle whose angle B = right-angle and AB = BC Prove that, (BC * cos C – AC * cos B)/(BC * cos B – AC * cos A) + cos C = 0
32. ABC is a right-angled triangle whose ZB- one right-angle. and cot A + cot B = 2cot C Prove that, A * C² + B * C² = 2A * B²

See more:

• Common tangent
• Principle of calorimetry