Today is our topic of discussion Review of the Theorem of Pythagoras .
Review of the Theorem of Pythagoras
About 600 years before the birth of the Christ, the renowned Greek scholar Pythagoras (570-495 BC) described an extremely important theorem about right angled triangles. This theorem was named after him and so known as the theorem of Pythagoras. But it was known even around 1000 years before Pythagoras.
Egyptian surveyors had possessed the knowledge about the theorem. The theorem of Pythagoras can be proved in many ways. Two of its proofs have been taught in lower secondary level. So we will skip its proof. Herein it will contain only its explanation and some brief discussion.
Theorem 1 (Theorem of Pythagoras).
In a right angled triangle the area of the square drawn on the hypotenuse is equal to the sum of the areas of the two squares drawn on the other two sides.
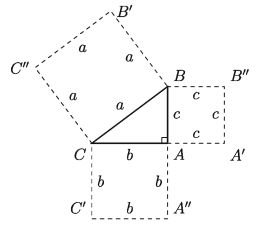
In the figure above ABC is a right angled triangle. <BAC is a right angle and BC is hypotenuse. If any square is drawn on the hypotenuse BC, its area is equal to the sum of the areas of the squares drawn on the sides adjacent to the right angle which are AB and AC.
Here BC² = the area of the square BB’C”C = a², AB² = the area of the square AA’B” B = c², and CA² = the area of the square CC’A”A = b².
Therefore, BC² = AB² + AC² or a² = b² + c².
For example, if the lengths of the two sides adjacent to the right angle of a right angled triangle are b = 8 cm. and c = 6 cm, it can be said as per the theorem of Pythagoras that the length of the hypotenuse will be a = 10 cm.
Similarly, it is possible to know the length of the third side by the lengths of any two sides.
Theorem 2 (Converse of the Theorem of Pythagoras)
If the area of the square on one side of a triangle is equal to the sum of areas of the squares drawn on the other two sides, the angle included by the latter two sides is a right angle.
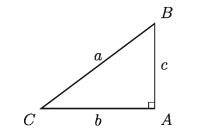
In the figure shown above, three sides of the triangle ABC are AB, BC and AC. The area of the square drawn on the side BC is equal to the sum of the area of the squares drawn on sides AB and AC. Therefore, B * C ^ 2 = A * B ^ 2 + A * C ^ 2 or, a ^ 2 = b ^ 2 + c ^ 2 So, angle BAC is a right angle. For example, we can say that if the lengths AB, BC and CA of triangle ABC are 6 cm., 10 cm. and 8 cm. respectively, angle BAC must be a right angle.
Since, AB² = 6² square cm .=36 square cm.,
BC²= 10² square cm .=100 square cm.,
AC² = 8² square cm .=64 square cm.,
B C² = 100 = 36 + 64 = AB²+ AC²
∠BAC = 90 ° = right angle.
Orthogonal Projection of a Point:
We call the orthogonal projection of any point on any definite straight line when it signifies the foot of the perpendicular drawn from that point on the definite straight line. Suppose, XY is a definite straight line and P is any point (figure below). We draw the perpendicular PP’ from the point P on the straight line XY and P’ is the foot of this perpendicular. So, the point P’ is the orthogonal of P on the line XY. The orthogonal projection of any point on any definite straight line is a point.

Orthogonal Projection of a Line:
Let, the end points of the line segment AB are A and B (figure above). Now the perpendiculars AA’ and B * B’ are drawn from the points A and B respectively on the line XY. The end points of the perpendiculars AA’ and BB’ are A’ and B’ respectively. This line segment A’B’ is the orthogonal projection of the line segmentAB on XY. Therefore, it is seen that the orthogonal projection is determined by drawing a perpendicular.
So, it is said that the line segment A’B’ is the orthogonal projection of the line segment AB on XY. In the figure above, if the line segment AB is parallel to XY, then AB = A’B’. From this conception, we can say that the perpendicular of the orthogonal projection on any line is a point. In that case, the length of the orthogonal projection is zero.
Note:
1. The foot of the perpendicular drawn from any point on any line is the orthogonal projection of that point.
2. The perpendicular of the orthogonal projection on any line is a point, whose length is zero.
3. Any definite line parallel to the line segment of the orthogonal projection will be equal to that line segment.

1 thought on “Review of the Theorem of Pythagoras”