Today is our topic of discussion Set exercises 1.1 .
Set exercises 1.1
1. (i) If any set has 2n elements, the number of its subsets will be 4xn.
(ii) Set of all rational numbers Q = {p/q p,q ∉z}.
(iii) a, b∉R; (a,b) = {x: x ∉R and a < x <b}.
Which combination of these statements is correct based on the information stated above?
1) i and ii
2) ii and iii
3) i and iii
4) i, ii and iii
If An={n, 2n, 3n,…} for every n Є N, answer the questions (2-4):
2. Which one of the following is the value of A,∩ A₂?
1) A1
2) A2
3) Ag
4) A4
3. Which one of the following denotes the value of A3 A6?
1) A2
2) A3
3) A
4) A6
4. Which one of the following is to be written down instead of A2 A3?
1) A3
2) A_{4}
3) As
4) A_{6}
5. Given that, U={ x : 1≤ x ≤ z} , , A= {x : x is an odd number} and B={x : x is a prime number}. List the following sets in tabular method:
1) A
2) B
3) C={ x : x ∉ in A and x ∉ B)
D={x : x ∉ in A or x ∉ B}
6. The number of elements of A and B are shown in the Venn Diagram below. If n(A) = n(B) then find out the value of 1 )x 2) n (A ∪ B)3) n (B / A)

7. If U={ x : x is a positive integer}, A= {x : x ≥ 5 } ⊂ U and B={ x : 5 x ⊂ 12 } U then find the value of n (A cap B) and n( A’ cup B) .
8. If U=\ x / x is an even integer), A= \{x / 3 * x >= 25\} subset U and B =\ x : 5x < 12 \ subset U then find n (A cap B) and n( A’ cap B^ prime )
9. Show that, 1) A backslash A= emptyset,2)A backslash(A backslash A)=A
10. Show that, A*(B cup C)= (AB) cup(A* C)
11. If A subset B and C subset D then show that, (AC) subset(B* D)
12. Show that, sets A=\ 1, 2, 3 ,***,n\ and B=\ 1, 2, 2 ^ 2 ,***,2^ n-1 \ are equivalent.
13. Show that, set of square of natural numbers \ 1, 4, 9, 16, 25, 36 ,***\ is an infinite set.
14. Prove that, if n(A) = p n(B) = q and A cap B= emptyset. then n(A cup B)= p + q .
15. Prove that, if A, B, C are finite sets, n(A cup B cup C)= n(A) + n(B) + n(C) – n (A cap B)-n(B cap C)-n(C cap A)+n(A cap B cap C).
16. A = \{a, b, x\} and B = \{c, y\} are subsets of the universal set U = \{a, b, c, x, y, z\}
1) Verify that, (i) AC B’ (ii) AU B’ = B’ (iii) A’n B = B. 2) Find out: (A cap B) cup(A cap B’ )
17. Out of 30 students of a class, 19 have taken Economics, 17 have taken Geography, 11 have taken Civics, 12 have taken both Economics and Geography, 4 have taken both Civics and Geography, 7 have taken both Economics and Civics, while 3 have taken all three subjects. How many students have taken none of the three subjects?
18. In the following Venn Diagram, universal set U =A cup B cup C.
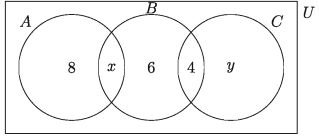
1) If n (A cap B)=n(B cap C), then find the value of x.
2) If n(B cap C’ )=n(A^ prime cap C). then find the value of y.
3) Find the value of n(U)
19. In the following Venn Diagram, U =A cup B cup C and n(U) = 50
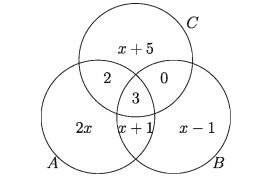
1) Find the value of x.
2) Find the value of n(B cap C’ ) and n( A’ cap B).
3) Find the value of n(A cap B cap C’ )
20. Three sets A, B and C are given in such a way that, A cap B= emptyset. A cap C= emptyset and C subset B Describe the sets by drawing a Venn Diagram.
21. Given that, A = {x: 2 < x ≤ 5, x = R}, B = {x: 1 ≤ x < 3, x = R} and C = {2,4,5). Express the following sets in set builder method: 1) An B
2) A’n B’
3) A’UB
22. Given that, U = {x: x < 10, x € R}, A = {x : 1 < x < 4} and B = {x: I 36}. Express the following sets in set builder method: 1) An B
2) A’n B 3) An B’ 4) A’n B’
23. Sets A and B are given below for each case. Find AUB and verify that AC (AUB) and B C (AUB).
1) A = {-2, -1, 0, 1, 2} and B = {-3,0,3}
2) A = {x: x = N, < 10 and x is the multiple of 2} and B = {x: x Є N, < 10 and x is the multiple of 3}
24. Find out An B in every case below and verify that, (An B) c A and (ANB) c B. 1) A = {0,1,2,3}, B = {-1,0,2} 2) A= {a, b, c, d}, B = {b,x,c,y}
25. Among the female students of Begum Rokeya College, a survey was conducted about their reading habits of the magazines the Bichitra, the Sandhani and the Purbani. It was found that 60% of the girls read the Bichitra, 50% read the Sandhani, 50% read the Pubani, 30% read the Bichitra and the Sandhani, 30% read the Bichitra and the Purbani, 20% read the Sandhani and the Purbani, while 10% read all three magazines.
1) What percentage of the girls do not read any of the three magazines?
2) What percentage of the girls read just two of the above magazines?
26. A= {x: x = R and x² – (a + b)x + ab = 0}, B = {1,2} and C = {2, 4, 5}
1) Find out the elelments of set A.
2) Show that, P(B˚C) = P(B) п P(C).
3) Prove that, Ax (BUC) = (A × B) u (A × C).
27. Out of 100 students of a class, 42 students play football, 46 play cricket and 39 play chess. Among them 13 play football and cricket, 14 play cricket and chess and 12 play football and chess. Besides, 7 students are not expert in any of these games.
1) Show the set of students who are expert in the above three games and expert in none of the games in Venn diagrram.
2) Find how many students are expert in all three games.
3) How many students are expert in at least one game? How many are expert in just two of the games?
28. Find out the set P(Ø), P({0}).
29. Once there was a mason in a village. He only built houses for those who did not construct their own house. Who built the house of the mason?
30. A= {x: x A). Describe briefly about the set A.
3 thoughts on “Set exercises 1.1”