Today our topic of discussion is Sets of Sets of Mathematics.
Sets of Mathematics

Sets and Functions
The term ‘set’ is well known to us. For example, dinner set, set of natural numbers, set of rational numbers etc. As a modern concept set has versatile use. The German mathematician George Cantor (1845-1918) first explained the concept of set.
He introduced the notion of infinite set, and created a sensation in mathematical science. His notion is now known as set theory. In this chapter we shall solve different problems by using concepts of set, diagrams and logic and idea of a function will also be introduced.
After completion of this chapter the learners will be able to express the concepts of sets and subsets through symbols.
‣ describe how sets can be expressed.
‣ define infinite sets, and distinguish between finite and infinite sets.
‣ define and verify union and intersection of sets. define power sets, and construct power sets of sets with two or three elements.
‣ define ordered pairs and cartesian products.
‣ prove simple set theoretic rules by using examples and Venn diagrams, and apply these rules for solving different problems.
‣ define relations and functions, and construct them. determine domain and range.
‣ draw diagrams for functions.
Sets
A set is simply a well organized object of real or imaginary world. For example, the set of three text books of Bangla, English and Mathematics. Some other
examples are the set of first 10 odd natural numbers, set of integers, set of real numbers etc. Sets are usually denoted by the capital letters of English alphabet like A, B, C ,…X,Y,Z.
For example, the set of three numbers 2,4,6 can be denoted by A = \{2, 4, 6\}
Each object or member of the set is called its element. For example, if B = \{a, b\} to express that a and b are its elements the sign E is used to express the element. a and b are elements of B;
a in B and we can read as a, is a member of B (a belongs to B) b in B is a member of b, (b belongs to B)
The above set B does not contain c. So it is expressed as c notin B and is read as c is not a member of B (e does not belong to B)
Methods for expressing sets
Sets can be expressed using two methods, namely Roster method or tabular method and Set Builder Method.
Roster method: In this method all members are listed and put inside {} and if there are more than one element, then elements are separated by commas. For example, A = \{a, b\} , B = \{2, 4, 6\} C=\ Niloy , Shuvro, Tisha} etc.
Set builder method: In this method all elements are not listed rather their common property is described. For example, A=\ x / x is an odd natural number \ B=\ x / x is the first five students of class IX} etc. Here, b v^ + :^ prime has been expressed such that. Since in this method element of the set is specified by rules, this method is called Rule Method.

Example 1. Express A = {7, 14, 21, 28} in set building method.
Solution: The elements of A are 7, 14, 21, 28.
Here, each element is a multiple of 7 and not exceeding 28.
∴ A= x : x , is a multiple of 7 and 0 < x ≤ 28
Example 2. Express B={ x : x , is a divisor of 28 } by using roster method.
Solution: Here, 28 = 1 * 28 = 2 * 14 = 4 * 7
∴ factors of 28 are 1, 2, 4, 7, 14, 28
∴ Hence the desired set is B = {1, 2, 4, 7, 14, 28}
Example 3. Express C = x:x positive integer and x² < 18 ) by using roster method.
Solution: 1, 2, 3, 4, 5,… are positive integers.
Here, if 1, then x ² = 1² = 1; if x = 2 then x ² = 2² = 4
If x = 3 then x ²= 3² = 9 ; if x = 4 then x² = 4² = 16
If x = 5 then x² = 5² = 25 ; which is greater than 18.
∴ as per conditions the acceptable positive integers are 1,2,3 and 4. ..the given set is C = {1, 2, 3, 4}
Work: Express
1) C = {- 9, – 6, – 3, 3, 6, 9} by using set building method.
2) Express B= y : y integer and y³ <= 18 by using set building method.
Finite Set
The set number of elements of which can be determined by counting is called finite set. For example, D = {x, y, z} E= {3, 6, 9 ,…,60}, F= {x : x prime and 30 < x < 70 } etc are finite sets. Here, set D contains 3 elements, set E 20 elements and set F 9 elements.
Infinite Set
The set elements of which cannot be exhausted by counting is called infinite set. For example, A= {x : x odd natural number}, set of natural numbers N = { 1, 2, 3, 4 ,…}, set of integers Z ={…,-3,-2,-1,0,1,2,3…} set of rational numbers Q = {a/b: a and b integer and b ≠0} set of rational numbers R etc are infinite sets.
Example 4. Prove that the set of all natural numbers is an infinite set.
Solution: The set of natural numbers N={1, 2, 3, 4, 5, 6, 7, 8 ,..}
The set A={ 1, 3, 5, 7 ,…}consisting of odd natural numbers from the set N
The set N B={ 2, 4, 6, 8 ,…} consisting of even natural numbers from the set
The set of numbers C={3, 6, 9, 12 ,..}multiple of 3 from N
Here, sets consisting of elements from N cannot be determined by counting. As a result A, B, C are infinite sets.
∴ N is an infinite set.
Work: Determine which ones are finite and which ones are infinite sets:
1) (3,5,7)
2) { 1, 2, 2² ,…2^ 10 }
3) { 3, 3², 3³ ,…}
4) { x: x integer and x < 4}
5) { p/q:p and q are mutually coprimes and q > 1}
6) { y : y ∈ N and y² < 100 < y³ }
Empty Set
If a set does not have any element, the set is said to be empty set, and is denoted by ∅ . For example, the set of three male students of Girl’s school, { x ∈ N : 10 < x < 11} ,{ x ∈ N : 2 prime and 23 < x < 29 } etc.
Venn-Diagram
John Venn (1834-1923) first expressed sets by using pictures. Here every set is represented by a geometric figure like rectangles, cicrles and triangles in a plane. These pictures have been named after John Venn.
Subset
A = {a, b} is a set. Sets {a, b}, {a}, {b} can be formed from the elements of this set. Again, we can form a subset ∅ with no elements at all. These sets {a,b}, {a}, {b},∅ are subsets of set A. All the sets that can be formed from a set are called subsets of the original set.
Subset is denoted by ⊆ . If B is a subset of A, then we write B ⊆ A. B is a subset of A. Among the subsets above {a, b} is equal to set A. Each set is the subset of itself, again in formed from any set
∴∅ is a subset of any set.
Let P = {1, 2, 3} and Q = {2, 3} R= {1,3}, then P, Q and R are subsets of P. That is, P ⊆ P ,Q ⊆ P and R ⊆ P
Proper Subset
Of the subsets constructed from a set, the ones that have lesser number of elements than the original set is called proper set. For example, A = {3, 4, 5, 6} and B = {3, 5} are two sets. Here all elements of B are also elements of A, and number of elements in B is less than that of A.
therefore B is a proper subset of A and is expressed as B ⊂ A.
In the examples of subsets Q and R are each proper subset of P. It may be mentioned here that is a proper subset of any set.
Example 5. Write down the subsets of P = {x, y, z} and identify those that are proper subsets.
Solution: Given, P = {x, y, z}
Subsets of P are {x, y, z}, {x, y}, {x, z}, {y, z}, {x}, {y\}, {z}, ∅.
Proper subsets of P are {x, y}, {x, z}, {y, z}, {x}, {y}, {z}, ∅
Observation: If number of elements of a set is n, then it has 2″ subsets, and number of proper subsets is 2 ^ n – 1
Equivalent Set
If two sets have the same elements, then they are said to be equivalent sets. For example, A = {3, 5, 7} and B = {5, 3, 3, 7} are two equivalent sets, then they are denoted by A = B Note that A = B if and only if A subseteq B and B subseteq A
Again, if A = {3, 5, 7} B = {5, 3, 3, 7} and C = {7, 7, 3, 5, 5} then sets A, B and Care equivalent sets. That is A = B = C
Observation: If order of elements in the set are changed or certain element is repeated set is not changed.
Difference of Sets
Let A = {1, 2, 3, 4, 5} and B = {3, 5} . If we delete the elements of set B from that of A, then we get (1,2,4) and is denoted by A backslash B or A – B and is read A delete B.
A – B = {1, 2, 3, 4, 5} – {3, 5} = {1, 2, 4}
Example 6. If P={ x 😡 is a factor of 12} and Q={ x : x is a multiple of 3 and x ≤ 12} , then determine P – Q
Solution: Given, P= { x : x is a factor of 12}
Here, factors of 12 are 1, 2, 3, 4, 6, 12
∴ P = {1, 2, 3, 4, 6, 12}
Again, Q={x : 3 is a factor of r and x ≤ 12 }
Here, multiples of 3 up to 12 are 3, 6, 9, 12
Q = {3, 6, 9, 12}
P – Q = {1, 2, 3, 4, 6, 12} – {3, 6, 9, 12} = {1, 2, 4}
∴ The required set is: {1,2,4)
Universal Set
All sets under discussion are subsets of a definite set. For example: the set A = {x, y} is a subset of the set B = {x, y, z} Here, B set is called as universal set with respect to set A. So if all sets under discussion are subsets of a given set, then the later set is said to be universal set with respect to sets under discussion.
Usually universal set is denoted by U. However, other symbols can also be used to denote universal set. For example, if set of all even natural numbers is C = \ 2, 4, 6 ,…\ and set of all natural numbers is N={ 1, 2, 3, 4, 5, 6 ,…} , then N will be universal set with respect to the set C.
Complement of a Set
Let U be universal set and A be a subset of U. Then the set of elements outside of A is termed as complementary set of A. The complementary set of A is denoted by A ^ c or A’. Mathematically, A ^ c =U backslash A.
A ^ c
Let, P and Q be two sets. Then the elements of P that are not elements of Q are said to form the complementary set of P with respect to Q. and is written Q ^ c =P backslash Q
Example 7. If U = {1, 2, 3, 4, 5, 6, 7} , A = {2, 4, 6, 7} and B = {1, 3, 5} then determine A ^ c and B ^ c.
Solution: A^ c =U \ A={ 1,2,3,4,5,6,7} \ {{2, 4, 6, 7} ={1, 3, 5} and B^ c =U \ B={ 1,2,3,4,5,6,7} \ {1, 3, 5\} = \{2, 4, 6, 7\}
The required sets are A ^ c = {1, 3, 5} and B ^ c = {2, 4, 6, 7}
Union of Sets
The set consisting of elements of two or more sets is said to be union of sets. Let, A and B be two sets. The union of sets A and B is denoted by A ∩ B and read as A∪ B. In set building method A ∩ B={x:x∈ A or x ∈ B}
Example 8. If C = {3, 4, 5} and D = {4, 6, 8} determine C ∪ D
Solution: Given C = {3, 4, 5} and D = {4, 6, 8}
C cup D={3,4,5} ∪ {4, 6, 8} = {3, 4, 5, 6, 8}
The set to be determined is: (3,4,5,6,8}
Intersection of Sets.
The set consisting of common elements of two or more sets is known as intersection set Let A and B be two sets. The intersection of sets A and B is denoted by A cap B and read as A intersection B. In set building notation A ∪ B={x:x ∈ A and x ∈ B}
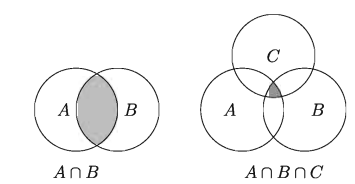
Example 9. If P={ x ∈ N : 2 < x ≤ 6 } and Q = { x ∈ N: x is even and x ≤ 8 } determine P ∩ Q.
Solution: Given,
Q ={x ∈ N : x is even and x≤ 8 }= {2, 4, 6, 8}
P={ x ∈ N: 2 < x ≤ 6 } ={ 3,4,5,6}
∴ P ∩ Q={3,4,5,6} ∪ {2, 4, 6, 8} = {4, 6} The set to be determined is {4,6}
∴ P∩Q
Disjoint Set
If there is no element common to any two sets, then these two sets are called disjoint sets. Let A and B be two sets. If A cap B= emptyset then A and B are said to be mutually disjoint sets.
Work: If U = {1, 3, 5, 9, 7, 11} E = {1, 5, 9} and F = {3, 7, 11} then determine E ^ c cup F^ c and E ^ c cap F^ c ,
Power Sets
A = {m, n} is a set. Subsets of A are {m, n}, {m}, {n}, emptyset, and set of all sets{{m, n}, {m}, {n} , ∅ } of A is called power set of A. Power set of A is denoted by P(A) . So the set formed by all subsets of a set is called power set of a given set.

Example 10. Find the number of elements of the power sets A = ∅, B = {a} , C = {a, b}
Solution: Here P(A) =∅
∴ number of elements of A is 0 and number of elements of its power set i = 1 = 2 ^ 0
Again P(B) ={{ a} , ∅}
∴ number of elements of B is 1, and number of eleemnts of its power set is = 2 = 2 ^ 1 and P(C)={{a}, \{b}, \{a, b} ,∅ }
∴ number of elements of C is 2 and number of elements of its power set 2 ^ 2 is = 4
So if number of elements of a set is n, then number of elements of its power set is 2 ^ n
