Today our topic of discussion is Similarity of Mathematics.
Similarity of Mathematics

Similarity
The congruence and similarity of triangles have been discussed earlier in class VII. In general, congruence is a special case of similarity. If two figures are congruent, they are similar; but two similar triangles are not always congruent.
Ratio, Similarity and Symmetry
Equiangular Polygons: If the angles of two polygons with equal number of sides are sequentially equal, the polygons are known as equiangular polygons.
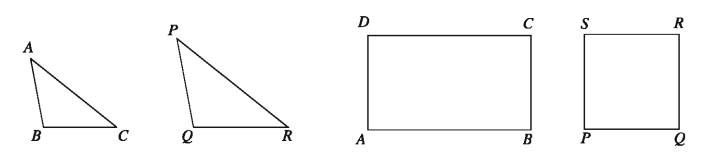
Similar Polygons: If the vertices of two polygons with equal number of sides can be matched in such a sequential way that
(2) The matching angles are equal and (ii) The ratios of matching sides are equal, then the two polygons are called similar polygons.
In the above figures, the rectangle ABCD and the square PQRS are equiangular since the number of sides in both the figures is 4 and the angles of the rectangle are sequentially equal to the angles of the square (all right angles).
Though the similar angles of the figure are equal, the ratios of the matching sides are not the same. Hence the figures are not similar. In case of triangles, situation like this does not arise. As a result of matching the vertices of triangles, if one of the conditions of similarity is true, the other condition automatically becomes true and the triangles are similar. That is, two similar triangles are always equiangular and two equiangular triangles are always similar.
If two triangles are equiangular and one of their matching pairs is equal, the triangles are congruent. The ratio of the matching sides of two equiangular triangles is a constant. Proofs of the related theorems are given below.
Theorem 32.If two triangles are equiangular, their matching sides are proportional.
Special Nomination: Let ABC and DEF be triangles with ∠A = ∠D, ∠B = ∠E and ∠C = ∠F We need to prove that, (AB)/(DE) = (AC)/(DF) = (BC)/(EF)
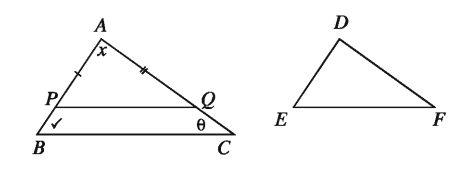
Drawing: Consider the matching sides of the triangles ABC and DEF unequal. Take two points P and Q on AB and AC respectively so that AP = DE and AQ = DF Join P and Q and complete the drawing.
Proof:
Step 1. In ΔAPQ and ΔDEF
AP = DE, AQ = DF , ∠A= ∠D
∴, ΔAPQ ≅ ΔDEF [SAS theorem]
∴, ∠APQ = ∠DEF= ∠ABC and ∠AQP = ∠DFE= ∠ACB.
That is, the corresponding angles produced as a result of intersections of AB and AC by the line segment PQ are equal.
Therefore PQ ||BC (AB)/(AP) = (AC)/(AQ) * c , (AB)/(DE) = (AC)/(DF) [corollary 1]
Step 2. Similarly, cutting line segments ED and EF from BA and BC respectively, it can be shown that,
(BA)/(ED) = (BC)/(EF) [theorem 28]
(AB)/(DE) = (AC)/(DF) = (BC)/(EF)
(AB)/(DE) = (BC)/(EF) The proposition opposite of theorem 32 is also true. i.e.
Theorem 33. If the sides of two triangles are proportional, the opposite angles of their matching sides are equal.
Special Nomination: Let, in ΔABC and ΔDEF prove that, ∠A = ∠D ∠B = ∠E, ∠C = ∠ F. (AB)/(DE) = (AC)/(DF) = (BC)/(EF) It is to.
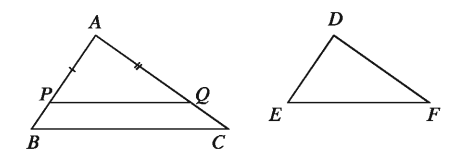
Drawing: Consider the matching sides of the triangles ABC and DEF unequal. Take two points P and Q on AB and AC respectively, so that AP = DE and AQ = DF Join P and Q.
Proof:
Since (AB)/(DE) = (AC)/(DF) Therefore (AB)/(AP) = (AC)/(AQ)
Therefore PQ ||BC [theorem 29]
∴∠ABC = ∠APQ [corresponding angles made by the transversal AB]
and ∠ACB = ∠AQP [corresponding angles made by the transversal AC]
∴ ΔABC andΔAPQ are equiangular.
∴ (AB)/(AP) = (BC)/(PQ) (AB)/(DE) = (BC)/(PQ) [theorem 32] [SSS theorem]
But (AB)/(DE) = (BC)/(EF) [supposition]
(BC)/(EF) = (BC)/(PQ)
∴EF = PQ
Therefore triangle APQ and triangle DEF are congruent.
∠ PAQ = ∠EDF, ∠APQ = ∠DEF, ∠AQP = ∠DFE
- ∠APQ = ∠ABC and ∠AQP = ∠ACB
angle A = ∠D ∠B = ∠E, ∠C = ∠F
Theorem 34. If one angle of a triangle is equal to an angle of the other and the sides adjacent to the equal angles are proportional, the triangles are similar.
Special Nomination: Let in ΔABC and ΔDEF . ∠A = ∠D and It is to be proved that, ΔABC and ΔDEF are similar. (AB)/(DE) = (AC)/(DF)
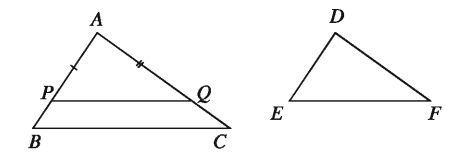
Drawing: Consider the matching sides of ABC and DEF unequal. Take two points P and Q on AB and AC respectively so that AP = DE and AQ = DF Join P and Q.
Proof:
For ΔAPQ and ΔDEF . AP = DE AQ = DFandi internal ZA = internal angle D ΔAPQ ≅ ΔDEF
[SAS theorem]
- ∠A = ∠D ∠APQ = ∠E, ∠AQP = ∠F Again, since .. PQ ||BC (AB)/(DE) = (AC)/(DF) therefore (AB)/(AP) = (AC)/(AQ)
Therefore ∠ABC = ∠APQ and ∠ACB = ∠ AQP
∴∠A = ∠D ∠B = ∠E. and ∠C = ∠F [theorem 29]
i.e. Δ ABC and Δ DEF are equiangular.
Therefore Δ ABC and Δ DEF are similar.
Theorem 35. The ratio of the areas of two similar triangles is equal to the ratio of squares on any two matching sides.
Special Nomination: Let the triangles ABC and DEF be similar and BC and EF be their matching sides respectively. It is required to prove that, triangle ABC : triangle DEF = B * C² / E * F²
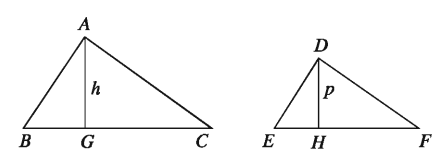
Drawing: Draw perpendiculars AG and DH on BC and EF respectively. Let AG = h DH = p
Proof:
Step 1. triangle ABC = 1/2 * BCh and triangle DEF = 1/2 * EFp (Delta*ABC)/(Delta*DEF) = (1/2 * BCh)/(1/2 * EFp) = h/p * (BC)/(EF)
Step 2. But in the triangles ABG and DEH, ∠B = ∠E. ∠AGB = ∠DHE [1 right angle]
∴ ∠BAG = ∠EDH
∴ Δ ABC and ΔDEF are equiangular, so similar.
∴h/p = (AB)/(DE) = (BC)/(EF)[as ΔABC and ΔDEF are similar]
Step 3. ΔABC ΔDEF = h/p * (BC)/(EF) = (BC)/(EF) * (BC)/(EF) = (B * C ^ 2)/(E * F²)
See more:
