Today is our topic of discussion Some Important Theorems .
Some Important Theorems
We shall now present the logical proof of some important theorems on the basis of the theorem of Pythagoras and by the conception of the orthogonal projection.
Theorem 3. The area of the square drawn on the opposite side of the obtuse angle of an obtuse angled triangle is equal to the total sum of the two squares drawn on the other two sides and product of twice the area of the rectangle included by either of the two other sides and the orthogonal projection of the other side.
Special Nomination:
Suppose, in the triangle ABC, ZBCA is an obtuse angle, AB is the opposite side of the obtuse angle and the sides adjacent to obtuse angle are BC and AC respectively.
CD is the orthogonal projection of the side AC on the extended side BC (figure below). It is to be proved that, AB² = AC² + BC2+2 BC CD
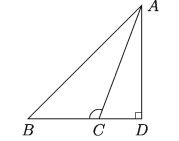
Proof:
As CD is the orthogonal projection of the side AC on the extended side BC, AABD is a right angled triangle and ZADB is a right angle.
So, according to the theorem of Pythagoras
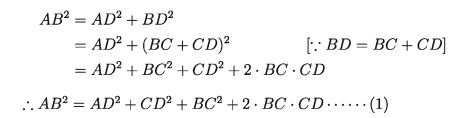
Again Δ is a right angled triangle and ZADC is right angle
AC² = AD² + CD² (2)
From the equation (2), putting the value AD² + CD² = AC² in equation (1), we get,
AB² = AC² + BC2 +2. BC. CD [Proved]
Theorem 4. In any triangle, the area of the square drawn on the opposite side of an acute angle is equal to the squares drawn on the other two sides diminished by twice the area of the rectangle included by any one of the other sides and the orthogonal projection of the other side on that side.
Special Nomination:
In the triangle ABC, ZACB is an acute angle and the opposite side of the acute angle is AB. The other two sides are AC and BC. Suppose, AD is a perpendicular on the side BC (left sided figure below) and the extended side of BC (right sided figure below). So, CD is the orthogonal projection of the side AC on the side BC in the case of both triangles. It is to be proved that AB2 = AC2+ BC2-2. BC. CD. [It is to be noted that here the perpendicular is drawn from A to BC. But similarly, the theorem can be proved by drawing a perpendicular from the point B to AC.]
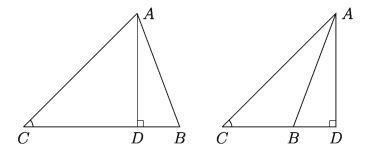
Proof:
ΔADB is a right angled triangle and ZADB is the right angle.
According to the theorem of Pythagoras, AB² = AD²+ BD²………..(1)
In the left sided figure above BD = BC . CD.
BD² = (BC – CD)² = BC² + CD² – 2. BC. CD
In the right sided figure above BD = CD – BC.
BD² = (CD – BC)² = CD² + BC2-2. CD. BC Therefore, in both figures, BD2 = BC2 + CD2-2. BC. CD… (2)
Now from equation (1) and (2), we get
AB² = AD²+ BC² + CD² – 2. BC.CD
Or, AB² = AD² + CD² + BC² −2. BC.CD ·……..(3)
Again, ΔADC is a right angled triangle and ZADC is the right angle.
According to the theorem of Pythagoras AC² = AD²+CD²…. (4)
from equation (3) and (4) we get, · (4)
AB² = AC² + BC²-2. BC. CD [Proved]
Remark:
1. In the case of the right angled triangle, the sides adjacent to the right angle are mutually perpendiculars, so each of their orthogonal projection is zero. If ZACB is a right angle then the orthogonal projection of AC on BC is CD = 0. So BC CD = 0, therefore AB2 = AC² + BC²
2. Theorem 3 and Theorem 4, are based on Theorem 1. That is why Theorem 3 and Theorem 4 are called extensions of Theorem 1, therefore they can be called extensions of the theorem of Pythagoras.
The decisions made on the basis of the explanation above: in the case of triangle ΔABC .
1) If ZACB is an obtuse angle,, A * B ^ 2 > A * C ^ 2 + B * C ^ 2
2) If ZACB is a right angle, A * B ^ 2 = A * C ^ 2 + B * C ^ 2
3) If angle ACB is an acute angle, A * B ^ 2 < A * C ^ 2 + B * C ^ 2
The following theorem is known as the theorem of Apollonius as this theorem was stated by Apollonius (240- 190 AD). It is established on the basis of the extensions of the theorem of Pythagoras (Theorem 3 and Theorem 4).
Theorem 5 (Theorem of Apollonius).
The sum of the areas of the squares drawn on any two sides of a triangle is equal to twice the sum of area of the squares drawn on the median of the third side and on either half of that side.
Special Nomination:
AD, Median of triangle triangle ABC bisects the side BC. It is to be proved that, AB² + AC²= 2(AD² + BD²) .
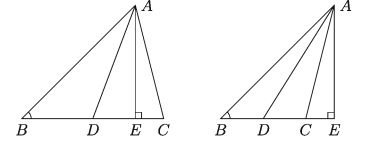
Proof:
We draw a perpendicular AE on the side BC (left sided figure above) and on the extended side of BC (right sided figure above). In both figures angle ADB is the obtuse angle of triangle ABD and DE is the orthogonal projection of the line AD on the extended BD.
As per the extension of the theorem of Pythagoras in the case of the obtuse angle [Theorem 3] we get,
AB²= AD²+ BD²+2* BD* DE……………..(1)
Here, angle ADC is an acute angle of triangle ACD and DC (left sided figure above) and DE is the orthogonal projection of the line AD on extended DC (right sided figure above).
As per the extension of the theorem of Pythagoras in the case of the acute angle [Theorem 4] we get,
AC²=AD²+ CD²- 2.CD.DE ………………(2)
Now adding the equations (1) and (2) we get,
AB²+ AC² = 2AD² + BD² + CD²+2. BD. DE – 2. CD. DE
= 2AD²+2BD2 [BD = CD]
AB² + AC² = 2(AD² + BD²) [Proved]
Determination of the relation between the side of the triangle and the median by the theorem of Apollonius.
Let, length of the sides of BC, CA and AB of the AABC are a, b and c respectively. AD, BE and CF are the medians drawn on sides BC, CA and AB and their lengths are d, e and ƒ respectively
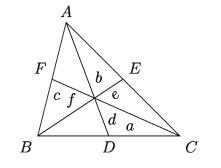
Then from Apollonius’s Theorem we get,
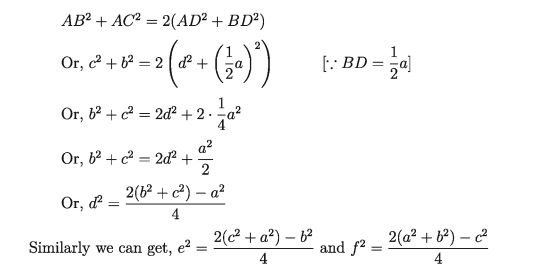
Therefore we can say that if the lengths of the sides of any triangle are known, the length of the medians can also be known.

2 thoughts on “Some Important Theorems”