Today our topic of discussion is The arc of a circle.
The arc of a circle

The arc of a circle
An arc is the piece of the circle between any two points of the circle. Look at the pieces of the circle between two points A and B in the figure. We find that there are two pieces, one comparatively larger and the other smaller.
The larger one is called the major arc and the smaller one is called the minor arc. A and B are the terminal points of this arc and all other points are its internal points. With an internal fixed point R the arc is called arc ARB and is expressed by the symbol ARB.
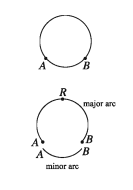
Again, sometimes minor arc is expressed by the symbol AB. The two points A and B of the circle divide the circle into two arcs. The terminal points of both arcs are A and B and there is no other common point of the two arcs other than the terminal points.
Arc cut by an Angle
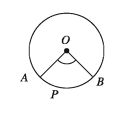
An angle is said to cut an arc of a circle if
- each terminal point of the arc lies on the sides of the angle,
- each side of the angle contains at least one terminal point and
- Every interior point of the arc lies inside the angle. The angle shown in the figure cuts the APB arc of the circle with centre O.
Angle in a Circle (Inscribed angle)
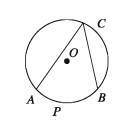
If two chords of a circle meet at a point on the circle then the angle formed between these chords is called circular angle or angle inscribed in a circle.
In the figure, ∠ACB is an angle in a circle. Every angle in a circle cuts an arc of the circle. This arc may be a major or minor arc or a semi-circle.
The angle in a circle cuts an arc of the circle and the angle is said to be standing on the cut off arc. The angle is also known as the angle inscribed in the conjugate arc.
In the adjacent figure, the angle stands on the arc APB and is inscribed in the conjugate arc ACB. It is to be noted that, APB and ACB are mutually conjugate.
Remarks: The angle inscribed in an arc of a circle is the angle with vertex in the arc and the sides passing through the terminal points of the arc. An angle standing on an arc is the angle inscribed in the conjugate arc.
Angle at the Centre (Central angle)
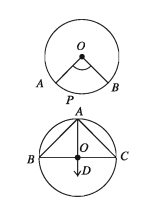
The angle with vertex at the centre of the circle is called an angle at the centre. An angle at the centre cuts an arc of the circle and is said to stand on the arc. In the adjacent figure, ∠AOB is an angle at the centre and it stands on the arc APB. Every angle at the centre stands on a minor arc of the circle.
In the figure APB is the minor arc. So the vertex of an angle at the centre always lies at the centre and the sides pass through the two terminal points of the arc. To consider an angle at the centre standing on a semi- circle the above description is not meaningful. In the case of semicircle, the angle at the centre ∠BOC is a straight angle and the angle on the arc ∠BAC is a right angle.
Theorem 20. The angle subtended by the same arc at the centre is double of the angle subtended by it at any point on the remaining part of the circle.

Given an arc BC of a circle subtending angles angle BOC at the centre O and ∠BAC at a point A of the circle ABC.
We need to prove that ∠BOC =2 ∠BAC
Drawing: Suppose, the line segment AC does not pass through the centre. In this case, draw a line segment AD at A passing through the centre.
Proof:
Step 1. In ∠AOB the external angle ∠BOD = ∠BAO+ ∠ABO exterior angle of a triangle is equal to the sum of the two interior opposite angles]
Step 2. In AAOB, OA = OB [ Radius of same circle]
Therefore, ∠BAO = ∠ABO [ Base angles of an isosceles triangle are equal]
Step 3. From steps (1) and (2), ∠BOD =2 ∠BAO
Step 4. Similarly, from ΔAOC . ∠COD =2 ∠CAO
Step 5. From steps (3) and (4),
∠BOD + ∠COD=2 ∠BAO+2 ∠CAO [by adding]
This is the same as ∠BOC =2 ∠BAC (Proved)
We can state the theorem in a different way. The angle standing on an arc of the circle is half the angle subtended by the arc at the centre.
Work: Prove the theorem 20 when AC passes through the centre O of the circle ABC.
Theorem 21. Angles in a circle standing on the same arc are equal.
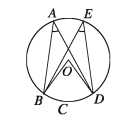
Let O be the centre of a circle and standing on the are BCD, ∠BAD and ∠ BED be the two angles in the circle. We need to prove that ∠BAD = ∠BED.
Drawing: Join O, B and O, D.
Proof:
Step 1. The arc ∠BCD subtends an ∠BOD at the centre O.
Therefore, BOD = 2∠BAD and∠BOD = 2∠BED [The angle subtended by an arc at the centre is double of the angle subtended on the circle]
:. 2∠BAD=2∠BED
or, ∠BAD = ∠BED (Proved)
Theorem 22. The angle inscribed in the semi circle is a right angle.
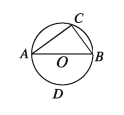
Let AB be a diameter of circle with centre at O and ∠ACB is the angle subtended by a semi circle. It is to be proved that ∠ACB is a right angle.
Drawing: Take a point D on the circle on the opposite side of AB of the circle where C is located.
Proof:
Step 1. The angle standing on the arc ADB ∠ACB= (straight angle in the centre ∠AOB) [. The angle standing on an arc at any point of the circle is half the angle at the centre]
Step 2. But the straight angle ∠AOB is equal to 2 right angles.
:. ∠ACB = (2 right angles) = 1 right angle (Proved).
Corollary 4. The circle drawn with hypotenuse of a right-angled triangle as diameter passes through the vertices of the triangle.
Corollary 5. The angle inscribed in the major arc of a circle is an acute angle.
Read more:
