Today our topic of discussion is Triangle of Mathematics.
Triangle of Mathematics

Triangle
A triangle is a figure closed by three line segments. The line segments are known as sides of the triangle. The point common to any pair of sides is the vertex. The sides form angles at the vertices.
A triangle has three sides and three angles. Triangles are classified by sides into three types: equilateral, isosceles and scalene.
By angles triangles are also classified into three types: acute angle d, right angle d and obtuse angled.
The sum of the lengths of three sides of the triangle is the perimeter. By triangle we also denote the region closed by the sides. The line segment drawn from a vertex to the mid-point of opposite side is known as the median. Again, the perpendicular distance from any vertex to the opposite side is the height of the triangle.

In the adjacent figure ABC is a triangle. A, B,C are three vertices. AB, BC CA are three sides and ∠ABC, ∠BCA, ∠CAB are three angles of the triangle. The sum of the measurement of AB, BC and CA is the perimeter of the triangle.
Equilateral triangle
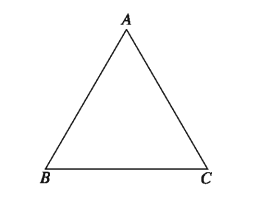
An equilateral triangle is a triangle of three equal sides. In the adjacent figure, ΔABC is an equilateral triangle; because, AB BC CA i.e., the lengths of three sides are equal.
Isosceles triangle

An isosceles triangle is triangle with two equal sides. In the adjacent figure ΔABC is an isosceles triangle; because AB AC BC i.e. the lengths of only two sides are equal.
Scalene triangle
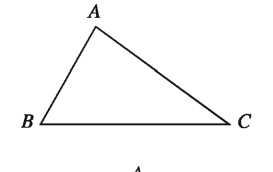
Sides of scalene triangle are unequal. ΔABC is a scalene triangle, since the lengths of its sides AB, BC, CA are unequal
Acute triangle
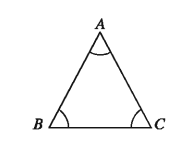
A triangle having all the three angles acute is acute angled triangle. In the ΔABC each of the angles ∠BAC,∠ABC, ∠BCA is acute i.e., the measurement of any angle is less than 90°. So ∠ABC is acute angled.
Right triangle
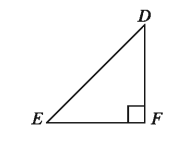
A triangle with one of the angles right is a right angled triangle. In the figure, the LDFE is a right angle; each of the two other angles ∠DEF and ∠EDF is acute. The triangle ADEF is a right angled triangle.
Obtuse triangle
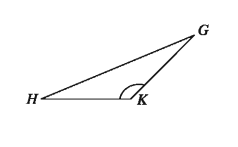
A triangle having an angle obtuse is an obtuse angled triangle. In the figure, the angle GKF is an obtuse angle; the two other angles ∠ GHK and ∠HGK are acute ΔGHK is an obtuse angled triangle.
Interior and Exterior Angles
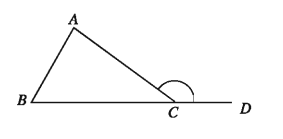
If a side of a triangle is produced, a new angle is formed. This angle is known as exterior angle. Except the angle adjacent to the exterior angle, the two others angles of the triangle are known as opposite interior angles.
In the adjacent figure, the side BC of triangle ABC is extended to D. The ∠ACD is an exterior angle of the triangle. ∠ABC , ∠BAC and ∠ACB are three
interior angles. ∠ACB is the adjacent interior angle 84 of the exterior angle ∠ACD Each of ∠ABC and ∠BAC is an opposite interior angle with respect to ∠ACD
Theorem 5. The sum of the three angles of a triangle is equal to two right angles.

Let ABC be a triangle. In the triangle ∠BAC+ ∠ABC+ ∠ACB = 2 right angles.
Draw CE from point C so that AB || CE.
Now ∠ABC = ∠ECD (corresponding angles] and ∠BAC = ∠ACE [alternate angles] , ∠ABC + ∠BAC= ∠ECD+ ∠ACE= ∠ACD
∠ABC+ ∠BAC+ ∠ACB= ∠ACD+ ∠ACB = 2 right angles.
Corollary 2. If a side of a triangle is produced, then exterior angle so formed is equal to the sum of the two opposite interior angles.
Corollary 3. If a side of a triangle is produced, the exterior angle so formed is greater than each of the two interior opposite angles.
Corollary 4. The acute angles of a right angled triangle are complementary to each other.
Work:
Prove that if a side of a triangle is extended, the exterior angle so formed is greater than each of the two interior opposite angles.
Congruence of Sides and Angles
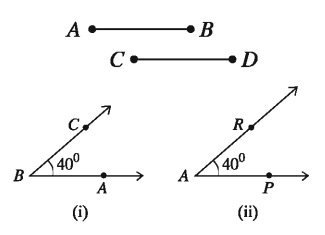
If two line segments have the same length, they are congruent. Conversely, if two line segments are congruent, they have the same length. If the measurement of two angles is equal, the angles are congruent. Conversely, if two angles B- are congruent, their measurement is the same.
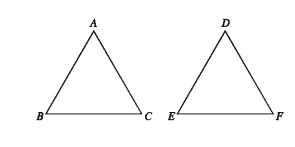
Congruence of Triangles
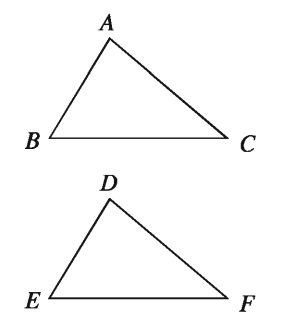
If a triangle when placed on another exactly covers the other, the triangles are congruent. The corresponding sides and angles of two congruent triangles are equal. In the adjacent figure, triangle ABC and triangle DEF are congruent.
If two triangles ΔABC and ΔDEF are congruent and vertices A, B, C superpose on vertices D, E, F respectively, then AB = DE, AC = DF,BC = EF and ∠A = ∠D,∠B = ∠E,∠C = ∠F . To express ΔABC and ΔDEF congruent it is written as ΔABC ≅ ΔDEF.
Theorem 6. (Side-Angle-Side criterion)
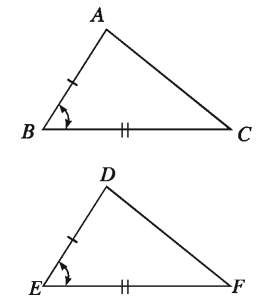
If two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle, the triangles are congruent.
Let ΔABC and ΔDEF be two triangles in which AB = DE, BC = EF and the included ∠ABC = the included ∠DEF Then, ΔABC ≅ ΔDEF .
Theorem 7. If two sides of a triangle are equal, the angles opposite the equal sides are also equal.
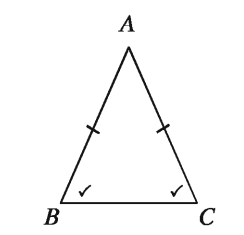
Suppose in the ΔABC, AB = AC Then, ∠ABC = ∠ACB
Theorem 8. If two angles of a triangle are equal, the sides opposite the equal angles are also equal.
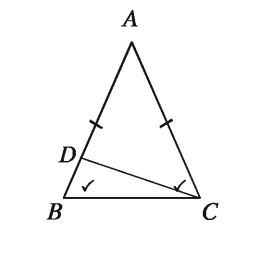
Special Nomination: Let, in the ΔABC, ∠ABC = ∠ACB. It is to be proved that, AB = AC.
Proof:
Step 1. If AB ne AC , then (i) AB > AC or, (i) AB < AC.
Suppose, (i) AB > AC Cut from AB a part AD equal to AC. Now, the ΔADC is an isosceles triangle. So,
∠ADC = ∠ACD
[The base angles of an isosceles triangles are equal]
In triangle DBC exterior angle ∠ADC > ∠ABC than each of the interior opposite angles]
[ matrix …\\ . matrix ] [Exterior angle is greater
.. ∠ACD > ∠ABC. Therefore, ∠ ACB > ∠ ABC but this is against the given condition.
Step 2. Similarly, (ii) if AB < AC it can be proved that ∠ABC > ∠ACB. but this is also against the condition.
Step 3. So neither AB > AC nor AB < AC
.. AB = AC (Proved)
Theorem 9. (SSS criterion) If the three sides of one triangle are equal to the three corresponding sides of another triangle, the triangles are congruent.
Let, in triangle ABC and triangle DEF , AB = DE AC = DF
and BC = EF Therefore, ΔABC ≅ ΔDEF
Theorem 10. (ASA criterion)
If two angles and the included side of a triangle are equal to two corresponding angles and the included side of another triangle, the triangles are congruent.
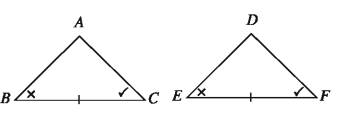
Let, in ΔABC and ΔDEF ∠B = ∠E ,∠C = ZF and the side BC = the corresponding side EF. Then the triangles are congruent, i,e: ΔABC ≅ ΔDEF
Theorem 11. (Hypotenuse-side criterion)
If the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle, the triangles are congruent.
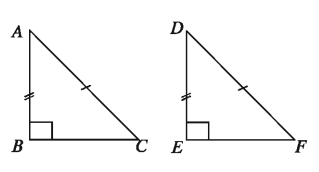
Let triangle ABC and triangle DEF be two right angled triangles, in which the hypotenuse AC = hypotenuse DF and AB = DE Then, ΔABC= ΔDEF
There is a relation between the sides and angles of a triangle. This relation is described in the following criteria 12 and 13.
Theorem 12. If one side of a triangle is greater than another, the angle opposite the greater side is greater than the angle opposite the lesser sides.
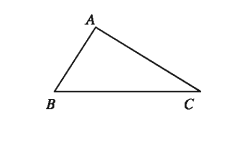
Let, in triangle ΔABC AC > AB Therefore ∠ABC > ∠ACB
Theorem 13. If one angle of a triangle is greater than another, the side opposite the greater angle is greater than the side opposite the lesser.
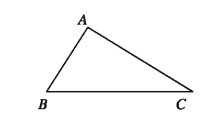
Special Nomination: Let, in triangle triangle ABC
∠ABC > ∠ACB It is to be proved that, AC > AB
Proof:
Step 1. If the side AC is not greater than AB, then (i) * AC = AB or, (ii) AC < AB
(i) If AC = AB then ∠ABC = ∠ACB triangle are equal]
[.. The base angles of isosceles
Which is against the supposition, since by supposition ∠ABC > ∠ACB (ii) Again, if AC < AB then ∠ ABC < ∠ ACB.
- The angle opposite to smaller side is smaller .But this is also against the supposition.
Step 2. Therefore, the side AC is neither equal to nor less than AB. therefore AC > AB (Proved).
There is a relation between the sum or the difference of the lengths of two sides and the length of the third side of a triangle.
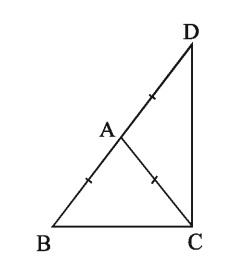
Theorem 14. The sum of the lengths of any two sides of a triangle is greater than the third side.
Let ABC be a triangle. Let BC be the greatest side of the triangle. Then, AB + AC > BC
Corollary 5. The difference of the lengths of any two sides of a triangle is smaller than the third side.
Let ABC be a triangle. Then the difference of the lengths of any two of its sides is smaller than the length of third side, i.e: AB – AC < BC
Theorem 15. The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and in length it is half.
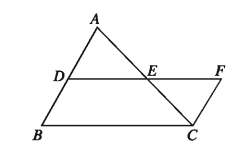
Special Nomination: Let ABC be a triangle. D and E are respectively mid-points of the AB and AC. It is required to prove DE ||BC and DE = 1/2 * BC
Drawing: Join D and E and extend to F so that EF = DE Draw a straight line segment from C to F. B
Proof:
Step 1. Between triangle ADE and triangle CEF AE = EC
[given]
DE = EF [by construction]
∠AED = ∠CEF [opposite angles]
Δ ADE ≅ Δ CEF [SAS theorem]
:. ∠ ADE = ∠ EFC [alternate angle]
.. AD ||CF
Again, BD = AD = CF and BD || CF
Therefore BDFC is a parallelogram.
.. DF | BC or, DE ||BC.
Step 2. Again, DF = BC or, DE + EF = BC
or, DE + DE = BC or, 2DE = BC or, DE = 1/2 * BC
DE ||BC and DE = 1/2 * BC Proved).
Theorem 16. (Pythagoras theorem)
In a right-angled triangle the square on the hypotenuse is equal to the sum of the squares of regions on the two other sides.
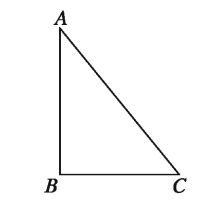
Let in the ΔABC, ∠ABC = 1 right angle and AC is the hypotenuse. Then, A * C²= A * B ² + B * C²
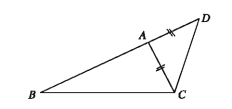
Example 1. In triangle triangle ABC . AB = AC BA is produced to D such that AD = AC C, D are added.
1) Draw the figure based on the stem.
2) Prove that, BC + CD > 2AC
3) Prove that, ∠BCD = 1 right angle.
Solution:
1)
2) Given, AB = AC and by construction AC = AD
For triangle BCD
BC + CD > BD [The sum of the lengths of any two sides of a triangle is greater than the third side.]
or, BC + CD > AB + AD
or, BC + CD > AD + AD
or, BC + CD > 2AD
∴BC + CD > 2AC
∴ AB = AC = AD
Given AB = AC Therefore ∠ABC = ∠ ACB
Hence ∠DBC = ∠ ACB
By construction AC = AD Therefore angle ADC = angle ACD
Hence ∠BDC = ∠ACD
In triangle ΔBCD .
∠BDC+∠DBC+∠BCD = 2 right angle [Sum of three angles of a triangle is equal to 2 right angles]
or, ∠ACD+ ∠ACB+ ∠BCD = 2 right angles
or, ∠BCD+ ∠BCD = 2 right angles
or, 2 ∠BCD = 2 right angles.
.. ∠BCD = 1 right angle
Example 2. PQR is a triangle. PA, QB and RC are three medians which intersect at point O.
1) Draw a figure based on the information.
2) Prove that, PQ + PR > QO + RO
3) Prove that, PA + QB + RC < PQ + QR + PR
Solution:
1)

2) From figure 1) it is to be proved that, PQ + PR > QO + RO
Proof: Any two sides of a triangle are greater than the third one.
In triangle triangle PQB PQ + PB > QB
Again in triangle ABOR, BR + BO > RO
PQ + PB + BR + BO > QB + RO
Or, PQ + PR + BO > QO + OB + RO
.. PQ + PR > QO + RO
3) Drawing: Produce PA to D such that PA = AD . Add Q, D.
Proof:
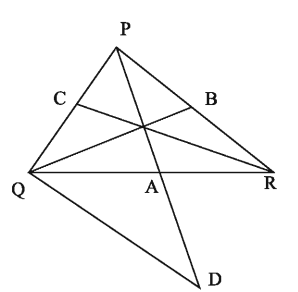
In triangle ΔQAD and ΔPAR, QA = AR,AD = PA
and the included ∠QAD = the included ∠PAR
∴ ΔQAD ≅ ΔPAR and QD = PR
Now, in Δ PQD, PQ + QD > PD or, PQ + PR > 2PA [ A is the mid point of PD]
Similarly, PQ + QR > 2QB, PR + QR > 2RC
PQ + PR + PQ + QR + PR + QR > 2PA + 2QB + 2RC or, 2PQ + 2QR + 2PR > 2PA + 2QB + 2RC
or, PQ + QR + PR > PA + QB + RC
∴ PA + QB + RC < PQ + QR + PR
Read more:
