Today is our topic of discussion Trigonometric Ratios .
Trigonometric Ratios
We discuss about trigonometrical ratios (sine, cosine, tangent, secant, cosecant, cotangent) of acute angle in this section. By the ratios of acute angle, we can determine the technique of any trigonometrical angle. Relation among the ratios and its sign in different quadrant can be explained. Some identity about trigonometric ratios are to be conceptualized. Trigonometrical ratios and the maximum or minimum values of trigonometric ratios of standard angle ( 0,π/6,π/4,π/3.π/2 ) are also included here.
(a) Trigonometrical Ratios of Acute Angle(Trigonometric Ratios of Acute Angles):
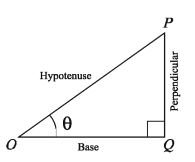
We consider a right angle triangle triangle ΔOPQ to discuss the trigonometrical ratios of acute angle. In triangle ΔOPQ . angle OQP is the right angle, OP is the hypotenuse of the side and angle POQ = theta is an acute angle subjected to angle ∠POQ . ∠OPQ the trigonometrical ratios of acute angle (sine, cosine, tangent, secant, cosecant, cotangent) are defined below:


(b) Trigonometric ratio of any angle:
Here we find the trigonometric ratios of any angle. For this we need to know the standard position of the angle. In Cartesian plane right side from origin that is considering the positive direction of r-axis as initial ray be obtained the position of the angle. Here we consider > as trigonometric angle and the limit of is boundless.
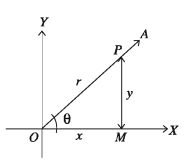
In Cartesian plane suppose X’ OX as x-axis, Y’OY as y-axis and O as origin. Angle is the product by revolving a ray OA in the anticlock-wise direction from Ө x-axis i.e. OX is the initial side and OA is the terminal side. (Following figure)
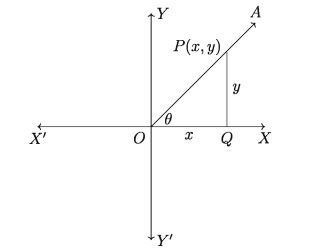
OX is called the initial side of the angle θ and OA is called the terminal side. Take a point P(x,y) different form O on the terminal side OA. So perpendicular distance of the point from OX is y, from OY is x and angle ∠OQP is a right angle (see the above figure).
Therefore, by Pythagoras, hypotenuse |OP| = r = sqrt(x ^ 2 + y ^ 2) So for any angle the trigonometric ratios will be:

Observation 1. As the point P and O are different so r = |OP| > 0 and sine and cose significant. The terminal side OA lie in x-axis then y = 0 and in that case cosece and coté is not defined.
Similarly terminal side OA lie in y-axis then x = 0 and in that case sece and tane is not defined.
Observation 2. Take another point P₁(x1,y1) different from P(x, y) (Following left and right figure) on the terminal side OA. Draw perpendicular PM and P₁M₁ from P(x, y) and P1(x1,y1) on x-axis. So, AOPM and AOP₁M₁ are similar.
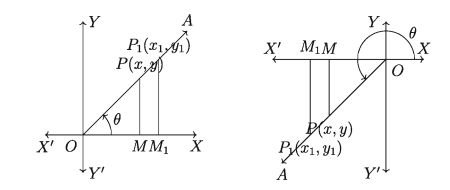
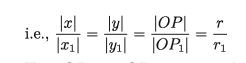
Here OP = r, OP₁ = r₁, ≈ and ₁ and y and y₁ are of the same
Decision:
Value of trigonometric ratios are not dependent upon the point P on
OA.
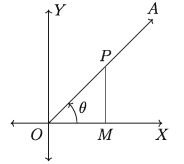
Observation 3. If 0 is an acute angle, the standard position of OA lies in the first quadrant and 0 = ZXOA (Figure beside). Take any point P(x, y) on OA and draw perpendicular PM on OX so that we can find the value of ratios from the discussion by (a) and (b) OM = x, PM = y and OP = r.
(c) Relations of the trigonometric ratios
From the definations of trigonometric ratios we see that,
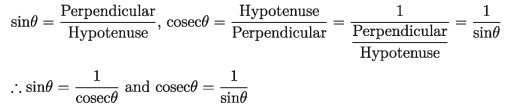
Similarly,
cosθ= (Base)/(Hypotenuse), secθ = (Hypotenuse)/(Base) = 1/((Base)/(Hvootenuse)) = 1/cos θ
i.e. cosθ= 1/(secθ)) and secθ= 1/(cosθ)
tanθ= 1/(cot θ)
Similarly, and cotθ= 1/(tanθ)
Some easy identities concerning about trigonometrical ratios
(Identities):
(i) sin^2θ + cos^2θ = 1
Proof: From the figure we see that,


From (1) we have, sin^2 theta = 1 – cos^2 theta or, cos^2 theta = 1 – sin^2 theta
Similarly it can be proved that,
(ii) 1 + tan^2 theta = sec^2 theta * or , sec^2 theta – 1 = tan^2 theta
(iii) 1+cot20 = cosec20 or, cosec²0-1 = cot20
See more:

3 thoughts on “Trigonometric Ratios”