Today is our topic of discussion Trigonometric ratios of many angles .
Trigonometric ratios of many angles
We discussed the technique about determining the ratios of an acute angle (0<θ<π/n) in the second part of trigonometry. Some easy identities are proved concerning relations of ratios. Sign of ratios in different quadrants, trigonometrical ratios of standard angles, idea of maximum and minimum values of ratios are conceptualized. Now we shall determine the ratios of negative angle (-θ) first. Based on them we will discuss the trigonometrical ratios of the angles π/2-θ,
π/2+θπ+θ+π-θ,3π-θ,2π-θ and nπ+θ and nπ/2-θ [ where n is positive integer and 0 < θ < π/2 ]
Trigonometric ratios of (−θ) where (0 < θ < π/2)
Suppose the revolving ray OA from its initial position OX produces angle ∠XOA =θ in anticlockwise direction in the 1st quadrant and in the same distance produces ∠XOA’ = – theta in clockwise direction (Figure below). Take a point P(x,y) on OA. Draw perpendicular PN on OX from P(x,y) . By extending PN it intersects OA’ on Q. So QN is the perpendicular on OX. As P(x,y) is in the 1 st quadrant then x > 0 , y > 0 and ON = x, PN = y .
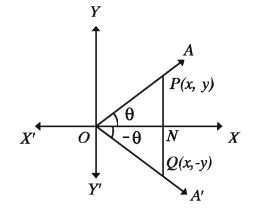
Now form the right angled triangle ΔOPN and ΔOQN, ∠PON = ∠QON. ∠ONP =∠ONQ and ON is common. So the triangles are equal.
PN = QN and OP = OQ
As the point Q is in the 4th quadrant, so the ordinate is negative. So the co-ordinates of Q is Q(x, – y) . In the right angled triangle OQN, ON = base, QN = perpendicular and OQ = hypotenuse = r (suppose).
So from the previous discussion we get,
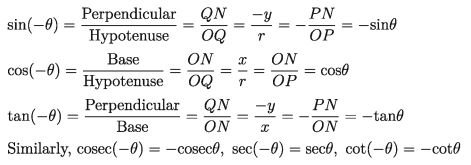
Observation: θ and (π/2-θ) are complement Angle. Complement of sine, tangent and cotangent are cosine, secant and cotangent.
Trigonometric ratios of (π/2+θ) where (0 < θ < π/2 ) :
Suppose revolving ray OA from its initial position OX produces ∠XOA = 0 in П the 1st quadrant in anticlock-wise direction and then produces ∠AOA’ in = π/2 in the same direction (Figure below).
So, ∠XOA = ∠YOA’ = θ and ∠XOA’ = π +θ.
Let any point P(x, y) on OA. Take a point Q on OA’ so that OP OQ. Draw = perpendicular PM and QN from P and Q on x-axis.
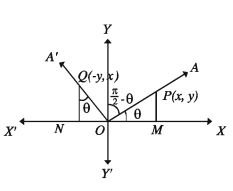
∠POM = ∠NQO = ∠YOQ = θ Q
Now from right angled triangle ΔPOM and ΔQON
ΔpΟΝ, <POM = NQO, PMO = QNO and
Now, if the co-ordinates of P is (x, y), then ON = -PM = -y and QN = OM = x
Co-ordinateofQ is Q(-y, x)
We get,
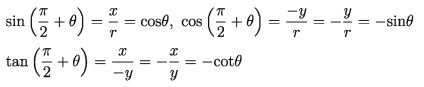
Similarly,
cosec(π/2+θ) = secθ, sec ( π/2+θ)=cosecθ
cot = (π/2+θ) =tanθ
Trigonometric ratios of (π + 0) where (0 < θ < π/2) :
Let the revolving ray OA from its initial position OX produces ∠XOA = in the 1st quadrant in anticlock-wise direction and then produces ∠AOA’ = π revolving in the same direction (Figure below). So, ∠XOA’ = (π+θ).
Now take any point P on OA and Q on OA’ so that, OP=OQ = r. Draw perpendicular PM and QN from P and Q on x-axis.
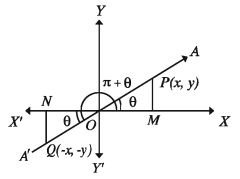
Now from the right angled triangles ΔPOM and ΔQON, ∠OMP ∠ONQ, ∠POM = ∠QON and OP=OQ= r. Therefore, triangles are similar.
PM QN and OM = ON
Now if the co-ordinate of P is (x, y), then ON: =-x, NQ=-y
Co-ordinatesofQ is (-x,-y)
i.e., sin(π + θ) = -y /r= -sinθ
COS (π + θ) =-x /r = -(r/x) -cosθ, tan(π + θ) = -y/-x =y/x
Similarly, cosec(π + θ) = -cosecθ
sec(+0)=-seco, cot(+0) cote
Method of determining the trigonometric ratios of (nx±0) where
π (0 <<):
Trigonometric ratios can be determined by the following steps.
Step 1. We are to divide the given angle into two parts whose one part is n multiple of П π ог 2 2 and the other part is an acute angle. i.e., we are to П express the given angle in the form (nx±0).
Step 2. If n is even the ratio remains the same, that is, sine remains sine, cosine remains cosine etc.
If n is odd the ratio will be changed, that is, sine, tangent and sec will be changed into cosine, cotangent and cosecant, cosine, cotangent.
Step 3. After knowing the position in the quadrant of (n × 7±0) put the sign of ratio determined in step 2 we have to Nota Bene: To determine the ratios students are advised to follow the method discussed here.

1 thought on “Trigonometric ratios of many angles”