Today our topic of discussion is Trigonometric ratios for the angles 30°, 45°, and 60°.
Trigonometric ratios for the angles 30°, 45°, and 60°
We have learnt how to draw angles 30 °, 45 °and 60 °in geometric way. Exact values of these trigonometric ratios for all these angles can also be determined geometrically.
Trigonometric ratios of the angles 30 °and 60 °

Let, ∠XOZ = 30 °and P is a point on OZ. Let us draw PM⊥OX and extend PM to Q so that MQ= PM. Add O, Q and extend to Z. Now for ΔPOM and ΔQOM, PM = QM
OM common side and included ∠PMO = included ∠QMO = 90 °
∴ ΔPOM ≅ΔQOM
∴ ∠QOM= ∠POM = 30 °
and ∠OQM = ∠OPM = 60°
Again, ∠POQ= ∠POM+ ∠QOM = 30°+ 30°= 60 °
∴ ΔOPQ is an equilateral triangle.
If OP = 2a then PM = 1/2 * PQ = 1/2 * OP = a [since ΔOPQ is an equilateral triangle.]
Form the right-angled ΔOPM we get,
OM = √(OP² – PM²) = √(4a²-a²)= √3a
Let us find the trigonometric ratios:

Trigonometric ratios for 45 °
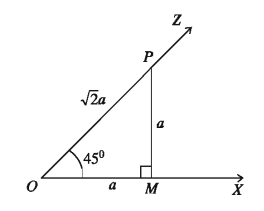
Let us assume ∠ XOZ = 45 °and P is a point on OZ.
Draw PM ⊥ OX
In the right-angled ΔOPM, ∠POM = 45°
∴ ∠OPM 45°
so PM = OM = a (denote)
Now, OP² = OM²+ PM² = a²+ a² = 2a²
or, OP = √2a
From the definitions of trigonometric ratios we get,
sin 45°= PM/OP =a/√2a = 1/√2 ; sin 45°= OM/OP =a/√2a = 1/√2
tan 45° = PM/OM= a/a =1
cosec45 ° = 1/(sin 45°) = √2 ; sec 45°= 1/(cos 45°) = √2
cot 45 °= 1/(tan 45°) = 1
Trigonometric ratios of complementary angles
We know, if the sum of two acute angles is 90 deg one of them is called complementary angle to the other. For example, 30° and 60°, and 15° and 75°are complementary angles to each other.
In general, the angles and (90°- θ) are complementary angles to each other. Let ∠ XOY = θ and P is the point on the side OY of the angle. We draw PM⊥OX . Since the sum of the three angles of a triangle is two right angles, therefore, in the right angled triangle POM, ∠PMO = 90 °
and ∠OPM + ∠POM= one right angle = 90°= 90° – θ
∠OPM 90°- ∠POM = 90°-θ [Since ∠POM = ∠XOY = θ]
sin(90 °- θ) = (OM)/(OP) =cos ∠POM=cos θ
cos(90° – θ) = (PM)/(OP) = = sin∠POM= sinθ
tan(90°-θ) = (OM)/(PM) = cot∠POM= cotθ
cot (90°-θ) = (PM)/(OM) = tan∠POM = tanθ
sec(90° – θ) = (OP)/(PM) = cosec∠POM = cosecθ
cosec(90° – θ) = (OP)/(OM) =sec ∠POM= sec θ
We can express the above formulae in words below:
sine of complementary angle = cosine of angle
cosine of complementary angle = sine of angle
tangent of complementary angle = cotangent of angle etc.
Trigonometric ratios of the angles 0° and 90°
We have learnt how to determine the trigonometric ratios for the acute angle of a right-angled triangle. Now, we see, if the angle is made gradually smaller, how the trigonometric ratios change. As @ get smaller the length of the side, PN also gets smaller. The point P closes to the point N and finally the angle 0 comes closer to the angle 0°, OP is reconciled with ON approximately.
When the angle comes closer to 0 deg the length of the line segment PN reduces to zero and in this case the value of sin theta= P overline N OP is approximately zero. At the same time, the length of OP is equal to the length of ON and the value of is 1 approximately. s*theta = (ON)/(OP)
The angle, 0 deg is introduced for the convenience of discussion in trigonometry, and the edge line and the original line of the angle 0 deg are supposed the same ray. Therefore, in line with the prior discussion, it is said that, cos 0 ^ a = 1 , sin 0 °= 0
If is the acute angle, we see tan θ= (sin θ)/(cos θ)
cot θ= (cos θ)/(sin θ) sec(θ) = 1/(cos θ) соsес θ= 1/(sin θ)
We define the angle 0° in probable cases so that, those relations exists.
tan 0 deg = (sin 0 °)/(cos 0 °) = 0/1 = 0 sec(0 °) = 1/(cos 0 °) = 1/1 = 1
Since division by 0 is not allowed, cosec 0 °cot 0° can not be defined.
Again, when the angle is very closed to 90 °hypotenuse OP is approximately equal to PN. So the value of sin theta is approximately 1. on the other hand, if the angle # is equal to 90 ^ 0 ON is nearly zero; the value of cos theta is approximately 0.
So, in agreement of formulae that are described above, we can say, cos 90 deg = 0
sin 90 °= 1
cot 90 °= (cos 90 °)/(sin 90 °) = 0/1 = 0
cosec(90 °) = 1/(sin 90 °) = 1/1 = 1
Since one cannot divided by 0 as before, tan 90° and sec 90° are not defined.
Note: For convenience of using the values of trigonometric ratios of the angles 0 °, 30 °, 45°,60 °and 90 °are shown in the following table:
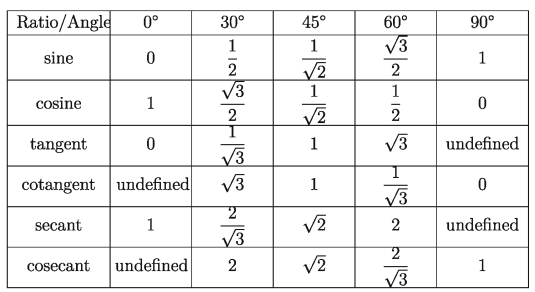
Observe: Easy method for remembering of the values of trigonometric ratios of some fixed angles.
(i) If we divide the numbers 0, 1, 2, 3 and 4 by 4 and take square root of the quotients, we get the values of sin 0 °, sin 30 °sin 45 °sin 60 °and sin 90° respectively.
(ii) If we divide the numbers 4, 3, 2, 1 and 0 by 4 and take square root of quotients, we get the values of cos 0 deg , cos 30°, cos 45 °cos 60 °and cos 90° respectively.
(iii) If we divide the numbers 0, 1, 3 and 9 by 3 and take square root of the quotients, we get the values of tan 0 ° tan 30 °tan 45 °and tan 60° respectively. (It is noted that tan 90 deg is undefined).
(iv) If we divide the numbers 9, 3, 1 and 0 by 3 and take square root of the quotients, we get the values of cot 30°, cot 45°, cot 60 °and cot 90° respectively. (It is noted that cot 0 °is undefined).
Example 13. Find the values:
1) (1 – sin²) (45 °))/(1 + sin² (45 °)) + tan² (45 °)
2) cot * (90 °)* tan(0 °)* sec(30 °) * cosec(60 °)
3) sin 60 °* cos 30 °+ cos 60 °* sin 30 °
4) (1 – tan²(60 °))/(1 + tan²(60 °)) + sin² (60 °)
Solution:
1) Given expression 1 = (1 – sin² (45 °))/(1 + sin² (45 °)) + tan² (45 °)
={1-(1/2 )²}{1+ (1/2 )²} +(1)². [sin 45° = 1 √2 and tan 45° = 1]
= (1 – 1/2)/(1 + 1/2) + 1 = (1/2)/(3/2) + 1 = 1/3 + 1 = 4/3
2) Given expression = cot 90 °tan 0 sec 30° cosec 60° = 0 * 0 * 2/(√3) * 2/(√3) = 0
[*] cot 90 ° = 0 tan 0 °= 0 , sec 30 °= 2/(√3)) cosec 60 °= 2/(√3) ]
3) Given expression = sin 60 °cos 30° + cos 60° – sin 30°
= (√3)/2 * (√3)/2 + 1/2 * 1/2
[ sin 60 °= cos 30 °= (√3)/2 , cos 60 °= sin 30 °= 1/2 ]
= 3/4 + 1/4 = 4/4 = 1
4) Given expression = (1 – tan²(60 °))/(1 + tan² (60 °)) + sin² (60 °)
= (1 – √3)²)/(1 + √3)²) + (√3)/2)² * 1 tan 60° √3, = sin 60° = (√3)/2 rfloor
= (1 – 3)/(1 + 3) + 3/4 = – 2/4 + 3/4
= (- 2 + 3)/4 = 1/4
Example 14. 1) If * √2* cos(A – B) = 1 , 2sin(A + B) = √3 and A, B are acute angles, find the values of A and B.
2) If(cos A – sin A)/(cos A + sin A) = (1 – √3/(1 +√3) find the value of A.
3) If A = 45 °Prove that, cos 2A = (1 – tan² A)/(1 + tan² A)
4) Solve: 2cos 0+3sin θ- 3 = 0 , where @ is an acute angle.
Solution:
1) √2 * cos(A – B) = 1 or ,cos(A-B)= 1 √2 ,cos(A-B)=cos 45° [*** cos 45 °= 1/(√2)]
∴ A – B =45° …(1) and 2sin(A + B) = √3 or, sin(A + B) = √3/2
or, sin(A+B)=sin 60° [ sin 60°=√3/2 ]
∴ A + B =60° …(2)
Adding (1) and (2), we get,
2A = 105°
A = (105°)/2 = 52 * (1°)/2
Again subtracting (1) from (2), we get,
2B = 15°
B = (15°)/2 = 7 * (1°)/2
Required A = 52 * (1°)/2 and B = 7 * (1°)/2
2) (cos A – sin A)/(cos A + sin A) = (1 – sqrt(3))/(1 + sqrt(3))
or, (cos A – sin A + cos A + sin A)/(cos A – sin A – cos A – sin A) [by addition-subtraction]
(2cos A)/(- 2sin A) = 2/(- 2√3
or, (cos A)/(sin A) = 1/√3
or, cot A = cot 60 °
∴ A = 60 °
3) Given that, A = 45 °
we have to prove that, cos2A = (1 – tan² A)/(1 + tan² A)
L.H.S.= cos 2A
= cos(2 * 45 °) = cos 90 °= 0
R.H.S.= (1 – tan² A)/(1 + tan² A)
= (1 – tan² (45 °))/(1 + tan² (45 °))
= (1 – (1)²)/(1 + (1)²)
= 0/2 = 0
∴ L .H.S.=R.H.S. (Proved)
(1 – √3) + (1 + √3)/(1 – √3) – (1 – √3)
4) Given equation 2cos² θ+ 3sinθ- 3 = 0
or, 2(1 – sin²θ) + 3sin θ – 3 = 0
or, 2(1 + sin θ)(1 – sin θ) – 3(1 – sin θ) = 0
or, (1 – sin θ)\{2(1 + sin θ) – 3\} = 0
or, (1 – sin θ)\{2sin θ- 1\} = 0
or, 2sin θ- 1 = 0
or, 1 – sin θ= 0
or, sin θ= 1
or, 2sin θ= 1
or, sin θ= sin 90°
or, θ= 90 °
or, sin θ= 1/2
or, sin θ= sin 30 °
or, θ= 30 °
is an acute angle, so θ= 30 °
See more:
