Today our topic of discussion is Trigonometric ratios of an acute angle.
Trigonometric ratios of an acute angle

Trigonometric ratios of an acute angle
Let ∠XOA be an acute angle. We take any point P on OA. We draw a perpendicular PM from the point P to OA. A right angled triangle POM is formed. The six ratios are obtained from the sides PM, OM and OP of ΔPOM which are called trigonometric ratios of the angle ∠XOA and each of them are named particularly.
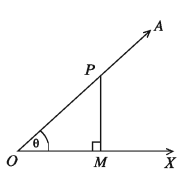
With respect to the ∠XOA of right-angled ΔPOM, PM is the opposite side, OM is the adjacent side and OP is the hypotenuse. Denoting ∠XOA =θ , the obtained six ratios are described below for the angle θ.
From the figure:
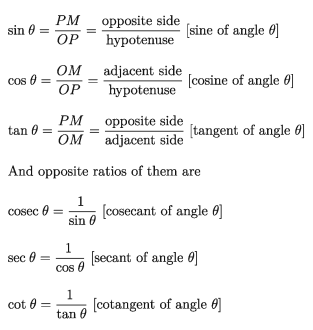
We observe, the symbol sin means the ratio of sine of the angle , not the multiplication of sin and θ. sin is meaningless without θ. It is applicable for the other trigonometric ratios as well.
Relation among the trigonometric ratios

FLet ∠XOA =θ is an acute angle.
rom the adjacent figure, according to the definition
sinθ=PM/OP,cosecθ=1/sinθ=OP/PM
cosθ=OM/OP,secθ=1/cosθ=OP/OM
tanθ=PM/OM,cotθ=1/tanθ=OM/PM
Again, tanθ PM/OM =(pm/op)/(om/op) [dividing the numerator and the denominator by OP ]
Or, tanθ = (sinθ)/(cosθ)
tanθ = (sinθ)/(cosθ)
and similarly,
cotθ = (cosθ)/(sinθ)
Trigonometric identity
(1) (sinθ)² + (cosθ)² = (PM/OP)²+ (OM/OP)²
PM² /OP² + OM² /OP²
= ( PM² + OM² )/OP²
=Op² /OP² [by the formula of Pythagoras]
=1
Or, (sin θ)² + (cos θ)² = 1 [ (sin θ)² + (cos θ)²= 1]
Remarks: For integer indices n we can write sin” for (sin θ)” and cos^n θ for * (cos θ) ^ n
(ii) sec²θ= (secθ)² = ((OP)/(OM)²
=Op²/OM²=(OM² + PM²)/ OM² [OP is the hypotenuse of right-angled ΔPOM]
=OM²/PM²+ OM²/OM²
=1+ (PM/OM)²=1+ (tan θ)²=1+tan²θ
[ sec²θ-tan²θ=1 ] and [tan²θ = sec²θ- 1]
(iii) cosec² = (cosec²0)² = (OP/PM)
=Op²/PM²=(PM²+OM²)/PM² [OP is the hypotenuse of right-angled ΔPOM [
=PM²/PM² + OM²/PM²
= 1 + (cot θ)² = 1 + cot² θ
Example 3. If tan A = 4/3 find the other trigonometric ratios of the angle A.
Solution:
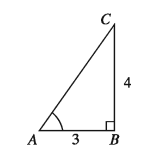
Given that, tan A = 4/3
So, opposite side of the angle A = 4 adjacent side= 3
hypotenuse = √(4² + 3²) = √25 = 5
Therefore, sin A = 4/5 cos A = 3/5 cot
A = 3/4
cosec A = 5/4 sec A = 5/3
Example 4. ∠B is the right-angle of a right angled ΔABC. If tan A = 1 then verify the truth of 2sin A.cos A = 1
Solution:
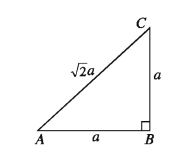
Given that, tan A = 1
So, opposite side of the angle adjacent side-a hypotenuse = √(a²+ a²) = √2 * a
Therefore, sin A = a/√2 * a
= 1/√(2 cos A
= a/√2 * a)
= 1/√2
Now, left hand side 2sin A.cos=A = 2 * 1/√2 * 1/√2
=1/2
= 1 = right hand side.
∴ 2sin A. cos A = 1 is true.
Example 5. Prove that, tanθ+ cotθ= secθ* cosecθ
Solution:
Left hand side = tan θ+ cot θ
= (sin θ)/(cos θ) + (cos θ)/(sin θ)
= (sin² θ+ cos² θ)/(sin θ* cos θ)
= 1/sin θ* cos θ [ sin² θ+ cos² θ= 1 ]
=1/sinθ*1/cosθ
=secθ*cosecθ
=Right hand sight
Example 6. Prove that, sec² θ+ cosec² θ= sec² θ* cosec² θ
L.H.S.= sec² θ+ co * sec² θ = 1/(1 + sin²θ) + (sin² θ)/(1 + sin² θ)
= 1/(sin θ) * 1/(cos θ) = co * sec(θ) * sec(θ)
= sec² θ* cosec² θ
= Right hand side (Proved)
Example 7. Prove that, 1/(1 + sin² θ) + 1/(1 + co * sec² θ) = 1
Solution:
L.H.S.= 1/(1 + sin²θ) + 1/(1 + co * sec² θ)
= 1/(1 + sin² θ) + 1/(1 + 1/(sin² θ)
= (1 + sin² θ)/(1 + sin² θ)
=1
=R.H. S(Proved)
Example 8. Prove that: 1/(2 – sin²θ) + 1/(2 + tan² θ) = 1
Solution:
L.H.S.= 1/(2 – sin²θ) + 1/(2 + tan² θ) = 1/(2 – sin²θ) + 1/(2 + (sin²θ)/(cos² θ))
= 1/(2 – sin²θ) + (cos²θ)/(2cos² theta +sin²θ)
= 1/(2 – sin²θ) + (cos² θ)/(2(1 – sin²θ) + sin²θ)
= 1/(2 – sin²θ) + (cos² θ)/(2 – 2sin²θ + sin²θ)
= 1/(2 – sin²θ) + (1 – sin²θ)/(2 – sin²θ)
= (2 – sin²θ)/(2 – sin²θ)
= 1 =R.H.S (Proved)
Example 9. Prove that: (tan A)/(sec(A) + 1) – (sec(A) – 1)/(tan A) = 0
Solution:
L.H.S.= (tan A)/(sec(A) + 1) – (sec(A) – 1)/(tan A)
= (tan² A – (sec² A – 1))/((sec(A) + 1) * tan A)
= (tan² A – tan² A)/((sec(A) + 1) * tan A) [:sec² A-1=tan² A]
= 0/((sec(A) + 1) * tan A)
=0=R.H. S(Proved)
Example 10. Prove that: √((1 – sin A)/(1 + sin A)) = secA – tan A
Solution:
L.H.S.= √((1 – sin A)/(1 + sin A))
= √((1 – sin A)(1 – sin A))/((1 + sin A)(1 – sin A))) [Multiplying the numerator and denominator by
√(1 – sin A)]
= √((1 – sin A)²)/(1 – sin² A))
= √(1 – sin A)²)/(cos² A)
= (1 – sin A)/(cos A)
= 1/(cos A) – (sin A)/(cos A)
= sec(A) – tan A
=R.H. S(Proved)
Example 11. If tan A + sin A = a and tan A – sin A = b prove that ,a² -b² = 4√(ab)
Solution: Here given that, tan A +sin A= a and tan A – sin A = b
L.H.S.= a ²- b ²
= (tan A + sin A)² – (tan A – sin A)²
=4tan A.sin A[** (a + b)² – (a – b)² = 4ab ]
= 4 √(tan² A * sin² A)
= 4√(tan² A * (1 – cos² A))
=4 √tan² A – tan² A .cos² A
= 4√(tan² A – sin² A) [** tan A= sin A cos A ]
= 4√((tan A + sin A)(tan A – sin A))
= 4√(ab)
=R.H. S(Proved)
Example 12. If sec A + tan A = 5/2 find the value of sec A – tan A
Solution: Here given that, sec A + tan A = 5 2 …( ) We know that, sec² A = 1 + tan² A
Or, sec² A – tan² A = 1
Or, (sec(A) + tan A)(sec(A) – tan A)
= 1 Or, 5/2 * (sec(A) – tan A)
= 1 [From (1)]
therefore sec A – tan A = 2/5
