Today is our topic of discussion Addition of Vectors.
Addition of Vectors
If from the terminal point of a vector u another vector v is drawn, then u + v denotes such a vector whose initial point is the initial point of u and terminal point is the terminal point of v
Let AB = u , vec BC = underline v be two vectors such that the terminal point of u is the initial point of y then the vector vec AC joining the initial point of u and the terminal point of v is called the sum of the vectors u and v and is denoted by u + v
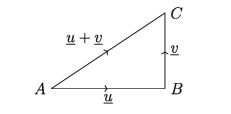
Triangle law of addition of vectors:
In the above diagram, if u and v are not parallel to each other then u, v and u + v vectors form a triangle; hence, this addition system is called triangle law. As a corollary to the triangle law of addition of vectors parallelogram law of addition of vectors is as follows:
Parallelogram law of addition of vectors:
If the magnitude and direction of two vectors u and u are denoted by the two adjacent sides of a parallelogram then the magnitude and direction of u + v is denoted by that diagonal of the parallelogram which passes through the point of intersection of the lines denoting the two vectors. We shall prove it now.
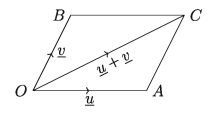
Proof:
Let OA and OB denote the vectors u and v drawn from any point O. Draw the parallelogram OACB and its diagonal OC . Then the diagonal vec OC of the parallelogram will denote the sum of u and v, i.e. overline OC = u + v .
In the parallelogram OACB, we have OB and AC equal and parallel. .. vec OB = dot v [by transfer of vectors]
Using triangle-law, u + v = vec OA + vec OB = vec OA + vec AC = OC [Proved]

Note: 1) The sum of two or more vectors is also said to be their resultant. The method of adition of vectors is followed in determining the resultant of forces or velocities. 2) If the two vectors are parallel, the parallelogram law is not applicable to their addition but the triangle-law is applicable in all the cases.
See more:

1 thought on “Addition of Vectors”