Today our topic of discussion is Area of Triangular region.
Area of Triangular region
Mensuration
The length of a line, the area of a place, the volume of a solid etc. are determined for practical purposes. In the case of measuring any such quantity, another quantity of the same kind having some definite magnitude is taken as unit. The ratio of the quantity measured and the unit defined in the above process is the amount of the quantity.
i.e. magnitude Quantity measured Unit quantity
In the case of a fixed unit, every measure is a number which denotes how many times the magnitude of the unit is the magnitude of the quantity measured. For example, the bench is 5 meter long. Here metre is a definite length which is taken as a unit and in comparison to that the bench is 5 times in length.
At the end of the Chapter, the students will be able to
‣ determine the area of polygonal region by applying the laws of area of triangle and quadrilateral and solve allied problems.
‣ determine the circumference of the circle and a length of the chord of a circle.
‣ determine the area of circle.
‣ determining the area of a circle and its segment, solve the alied problems.
‣ determine the area of solid rectangles, cubes and cylinder and solve the allied problems.
‣ determine the area of uniform and non-uniform solids
Area of Triangular region
In the previous class, we learned that area of triagular region => base x height.
- Right-angled triangle:
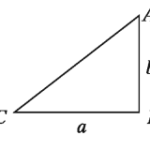
Let in the right-angled triangle ABC, BC = a and AB = b are the adjacent sides of the right angle. Here if we consider BC as the base and AB as the height, Area of ΔABC=1/2 x base x height =1/2 x ab
- Two sides of a triangular region and the angle included between them are given:

Let in triangle ABC the sides are BC = a CA = b AB = c AD is drawn perpendicular from A to BC. Let altitude (height) * AD = h
Considering the angle C we get, (AD)/(CA) = sin C
or, h/b = sinC
or, h= bsinC
Area of ΔABC = 1/2 * BCxAD
= 1/2a xbsinC =1/2 absinc
Similarly, area of ΔABC
= 1/2 * bc * sin A = 1/2 * ca * sin B
- Three sides of a triangle are given:
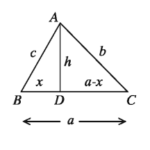
Let in ΔABC, BC = a , CA = b and AB = c
∴ Perimeter of the triangle 2s = a + b + c
We draw AD ⊥ BC
Let, BD = x then CD = a – x
In right-angled ΔABD and ΔACD
∴ A * D² = A * B ² – B * D² and A * D² = A * C² – C * D²
∴A * B² – B * D² = A * C² – C * D²
or, c² – x² = b² – (a – x)²
or, c² – x² = b² – a² + 2ax – x²
or, 2ax = c² + a² – b²
x = (c² + a² – b²)/(2a)
Again,
A * D² = c² – x ²
= c² – ((c² + a² – b²)/(2a))²
= (c + (c² + a² – b²)/(2a))(c – (c² + a² – b²)/(2a))
= (2ac + c² + a² – b²)/(2a) * (2ac – c² – a² + b ²)/(2a) = (\{(c + a)² – b²\}\{b² – (c – a) ²\})/(4a²)
= ((c + a + b)(c + a – b)(b + c – a)(b – c + a))/(4a²)
= ((a + b + c)(a + b + c – 2b)(a + b + c – 2a)(a + b + c – 2c))/(4a²)
= (2s(2s – 2b)(2s – 2a)(2s – 2c))/(4a²)
= 4s(sa) (sb) (sc) a2
AD = 2/a * √(s(s – a)(s – b)(s – c))
∴ Area of ΔABC
= 1/2 * BCAD = 1/2 * a * 2/a * √(s(s – a)(s – b)(s – c)) = √(s(s – a)(s – b)(s – c))
- Equilateral triangle:
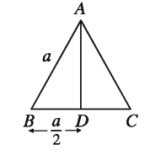
Let the length of each side of the equilateral triangular region ABC be a..
Draw AD ⊥ BC
∴ BD = CD = u/a In right-angled AABD B * D² + A * D² = A * B² sr, A * D ² = A * B² – B * D² = a ² – (a/2)² = a² – (a²)/4 = (3a²)/4
. AD = (√(3) * a)/2
Area of ΔABC = 1/2 * BCAD = 1/2 * a * (√(3) * a)/2 = (√(3))/4 * a²
- Isosceles triangle: Let ABC be an isosceles triangle in which
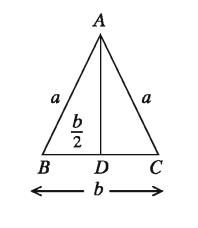
AB = AC = a and BC = b
Draw AD ⊥ BC . BD = CD = b/2
ΔABD is right angled. :. A * D² = A * B² – B * D²
= a² – (b/2)²= a² – (b²)/4 = (4a² – b²)/4 . AD = (√(4a² – b²))/2
Area of isosceles triangle ABC = 1/2 * BCAD (√(4a² – b²))/2 = b/4 * √(4a² – b²
Example 1. The lengths of the two sides of a right-angled triangle, adjacent right angle are 6 cm and 8 cm respectively. Find the area of the triangle.
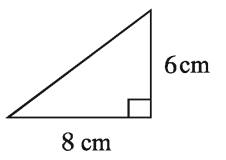
Solution: Let, the sides adjacent to right angle are a = 8 cm and b = 6 cm respectively
∴ Its area = 1/2 * ab = 1/2 * 6 * 8 square m = 24 square cm
Example 2. The lengths of the two sides of a triangle are 9 cm and 10 cm respectively and the angle included between them is 60 °. Find the area.
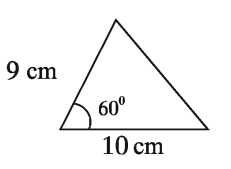
Solution: Let, the sides of triangle are a = 9 cm. and b = 10 cm. included angle θ= 60°
∴ Area of tringle = 1/2 * ab * sin 60°
= 1/2 * 9 * 10 * (√(3))/2 * sq cm = 38.97sq cm (approx.)
Required area 38.97 sq cm ( approx .)
Example 3. The lengths of the three sides of a triangle are 7 cm, 8 cm and 9 cm. respectively. Find its area.
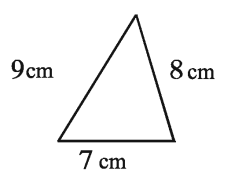
Solution: et, the lengths of the sides of the triangle are and c = 9 cm. a = 7 cm., b = 8 cm
Semi perimeter s = (a + b + c)/2 = (7 + 8 + 9)/2 cm = 12 cm
∴ Its area = √s(sa)(sb)(sc)
= √(12(12 – 7)(12 – 8)(12 – 9)) * sq .c pi
= √(12 * 5 * 4 * 3) sq.c m
= √720
= 26.83 sq. cm (approx.) –
∴ The area of the triangle 26.83 sq. cm (approx.)
Example 4. The area of an equilateral triangle increases by 3sqrt(3) sq. metre when the length of each side increases by 1 metre. Find the length of the side of the triangle.
Solution:
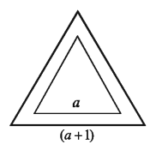
Let, the length of each side of the equilateral triangle is a metre
∴ Its area = (√(3))/4 * a² * sq . metre.
The area of the triangle when the length of each side increases by 1metre = (√(3))/4 * (a + 1)²* sq . metre.
According to the question, (√(3))/4 * (a + 1)² – √3/4 * a²= 3√3
or, (a + 1)² – a² = 12 [divi * dingby * (√(3))/4]
or, a² + 2a + 1 – a² = 12
or , 2a = 11 or, a = 5.5
The required length is 5.5 metre.
Example 5. The length of the base of an isosceles triangle is 60 cm. If its area is 1200 sq. met re, find the length of equal sides.
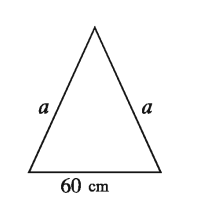
Solution: Let the base of the isosceles triangle be b = 60 cm and the length of equal sides bea.
Area of triangle = b/4 * √(4a² – b²)
According to the question, b/4 * √(4a² – b²) = 1200
or, 60/4 * √(4a² – (60)²) = 1200
or, √(4a² – 3600) = 1200
or, √(4a² – 3600) = 80
or, 4a² – 3600 = 6400 [by squaring]
or, 4a² = 10000
or, a² = 2500
∴ a = 50
The length of equal sides of the triangle is 50 cm.
Example 6. From a certain place two roads run in two directions making an angle of 120°. From that place, persons move in the two directions with speed of 10 km per hour and 8 km per hour respectively. What will be the direct distance between them after 5 hours?
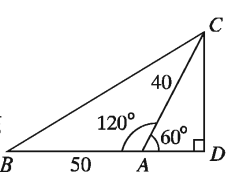
Solution: Let two persons start from A with velocities 10 km/hour and 8 km/hour respectively and reach B and C after 5 hours. Then after 5 hours, the direct distance between them is BC. From C perpendicular CD is drawn on BA produced.
∴ AB = 5 * 10km = 50 km, AC = 5 * 8km = 40km
and ∠BAC = 120 °
∴ ∠DAC = 180 °- 120 °= 60 °
ΔACD is right-angled.
(CD)/(AC) = sin 60 ° , CD = AC * sin 60 °=40* √3 2, =20 √ 3
and (AD)/(AC) = cos 60 °* or, AD = AC * cos 60 °= 40 * 1/2 = 20
Again, from right-angled triangle BCD we get,
B * C² = B * D² + C * D²= (BA + AD)² + C * D² = (50 + 20)² + (20√(3))² = 4900 + 1200 = 6100
∴ BC = 78.1 (approx.)
The required distance is 78.1 km (approx.)
Example 7. Consider the diagram given and –
1) Find the length of the side BC.
2) Find the value of BD?
3) Find the ratio of areas of AABD and ΔBCD .
Solution:
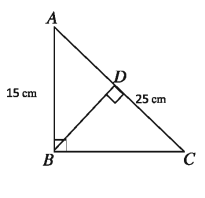
1) AB = 15, AC = 25
∴BC = √(A * C² – A * B²) = √((25)² – (15)²) = √(400) = 20
2 ) Area of ΔABC = 1/2 * BC.AB = 1/2 * AC.BD
1/2 * AC.BD = 1/2 * BC.AB
25*BD = 20 * 15
∴BD = 12
3) From right-angled triangle ΔABD we get, A * D² + B * D² = A * B²
or, A * D² + 12² = 15²
or, A * D² = 225 – 144 = 81
∴ AD = 9 and CD = AC – AD = 25 – 9 = 16
So, ratio of areas of ΔABD and ΔBCD is:
ΔABD/ΔBCD = (1/2 * BD.AD)/(1/2 * BD.CD) = 9/16
ΔABD: ΔBCD=9:16
See more:
