Today is our topic of discussion Binomial coefficient .
Binomial coefficient
The coefficient of different powers of y on the above expansion is called Binomial Coefficients. 1 is considered as the coefficient of y. If we arrange the coefficients of the above expansion,
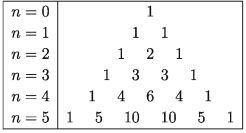
If we observe we see, the coefficients have formed a triangular shape. The technique of determining the coefficients of binomial expansion was first used by Blaise Pascal. So it is called Pascal’s Triangle. We can easily determine the coefficients of binomial expansion by pascal’s triangle.
Use of Pascal’s Triangle
From Pascal’s Triangle, we see that 1 is in both left and right side. The middle term of the triangle is the summation of two number just above the numbers. If we observe the following example, we can easily understand it.
Binomial coeffecients for n = 5 n = 6 will be:

(1+y)^5=1+5y+10y² + 10y³+5y^4 + y^5
(1+ y)^6 = 1 + 6y+15y²+20y³ + 15y^4+6y^5+ y^5
(1+y)^7=1+7y+21y² +35y³ + 35y^4 +21y^5+ 7y^6+y^7
If we observe carefully, we will understand that this method has a special weakness. For example, if we are to determine the expansion of (1+y)5, we need to know the expansion of (1+y). Again it is necessary to know preceeding two coefficients just above for any binomial coefficients.
To get relief from this position we want to directly find out the technique for determining the binomial coefficients. From Pascal’s Triangle we see that the power of coefficient of binomial expansion depends on power n and position of the term. We consider a new symbol (” where the power n and the position of the term r are related. For example if n = 4, the number of terms will be 5. We write the terms like this:
When n = 4, number of terms is 5: T1, T2, T3, T4, T5
Coefficients of them are: 1, 4, 6, 4, 1
Using new symbol:
(4), (4), (2), (13). (4)
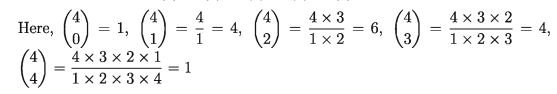
[You will understand easily from Pascal’s triangle.] Using new symbol ( n = 1, 2, 3 ,***) Pascal’s Triangle will be like this:
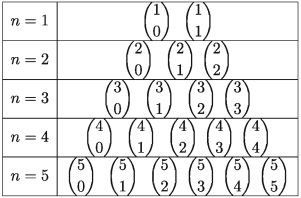
Therefore from the triangle above we can easily say that coefficient of third term T(2+1) (4,2) and coefficient of third (T 2 + 1 ) and fourth (T 3+ 1 ) of (1 + y) ^ 5 (T 2 + 1 ) of (1+y) are binomial(5,2) and binomial(5,3) respectively. Generally, coefficients of (r + 1) * th term (T r + 1 ) of
(1 + y) ^ n is binomial(n,r)
Now, to know the value of binomial(n,r) we again observe the Pascal’s Triangle. From the two sides of Pascal’s Triangle, we see that
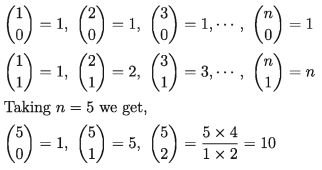
(5,3) = (5 x 4 x 3)/(1 x 2 x 3) = 10 (5,4) = (5 x 4 x 3 x 2)/(1 x 2 x 3 x 4) = 5
(5,5) = (5 x 4 x 3 x 2 x 1)/(1 x 2 x 3 x 4 x 5) = 1
Therefore, in case of (5,3) it can be said, (5,3) = (5(5 – 1)(5 – 2))/(1 x 2 x 3) and (6,4) = (6×6 – 1)(6 – 2)(6 – 3))/(1 x 2 x 3 x 4)
Generally, we can write,
(n,0) = 1, (n,n) = 1
( n, r) = n(n – 1)(n – 2) (n-r+1) 1x2x3x4x r
Using appropriate sign,

See more:

2 thoughts on “Binomial coefficient”