Today our topic of discussion is Decimal Fractions.
Decimal Fractions

Decimal Fractions
Each real number can be expressed in decimal fractions. For example, 2 = 2.0,2/5 = 0.4,1/3= 0.333… etc. Decimal fractions are of three types, = 3 namely: finite, repeated and infinite decimal fractions.
Finite decimal fractions: In any finite decimal fraction there is only a finite numbers of digits after the decimal point. For example, 0.12, 1.023, 7.832, 54.67,… etc are finite decimal fractions.
Repeated decimal fractions: In any repeating decimal fraction all or some digits on the right of decimal point come again and again. For example, 3.333…, 2.454545…, 5.12765765… etc are repeated decimal fractions.
Infinite decimal fractions: In an infinite decimal fraction digits on the right of decimal point never terminate, i.e. the number of digits on the right of the decimal point will not be finite neither will its part appear repeatedly. For example, 1.4142135, 2.8284271… etc are Infinite decimal fractions.
Remarks: Finite and repeating decimal fractions are rational numbers whereas infinite decimal numbers are irrational numbers. Value of any irrational number can be determined up to any desired decimal place. If numerator and denominator of a fraction can be represented by natural numbers, then the fraction is a rational number.
Repeating decimal fractions
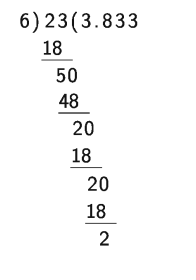
Express the fraction 23 into decimal 6 fraction. Observe that when numerator was divided by denominator the division process could not be completed. Observe that in the result the digit 3 appears over and over again. again. So 3.8333… is repeating decimal number.
The decimal fraction for which the same digit or a set of digits in order appear after decimal point is called repeating decimal fraction. The part of the repeating decimal fraction that appears over and over again is called repeating. The remaining part is nonrepating.
In a repeating decimal fraction if a single digit repeats, then a point is marked above that digit. Otherwise point is marked on the first and the last repeating digits. For example, 2.555… is written as 2.5 and 3.124124124… as 3.124.
In a decimal number if every digit after decimal point is repeating, then it is called a pure repeating fraction. Otherwise the fraction is called mixed. For example, 1.3 is a pure repeating fraction and 4.235112 is a mixed repeating fraction.
If in the denominator there are digits other than 2, 5 as a factor, then no numerator will be divisible by that denominator. Since there cannot be any digit other than 1, 2, …, 9 at some stage as residue, the same numbers will appear. Number of digits in the repeating part is always less than the number in the denominator.
Example 3. Express 3/11 and 95/37 into decimal fractions.
Solution: 3/11 and 95/37 have been converted into decimal fractions as below.
Actually 3 has been divided. But since 3 is smaller than 11, 0 has been placed in the dividend and a 0 has been placed to the right of 3 and made it 30.


Desired decimal fractions are respectively 0.27 and 2.567.
Converting repeating decimal fractions into common fractions
Example 4. Convert 0.3, 0.24, and 42.3478 into common fractions.
Solution: In the following, 0.3, 0.24 and 42.3478 have been cnverted into common fractions.

Explanation: From the three examples above it appears that,
- Repeating fraction is multiplied with a number equalling 1 followed by as many Os as there are digits after decimal point of a repeating fraction.
- The repeating decimal fraction has been multiplied with a number equalling 1 followed by as many Os as many nonrepeating digits are there in the repeating decimal fraction.
- Subtracting the second number from the first results in a whole number. It may be noted that nonrepeating part has been subtracted from the repeating decimal fraction by deleting decimal point and repeating point.
- The result of subtraction has been divided by a number equalling as many 9s as many repeating digits were there in the original repeating decimal fraction, followed by as many Os as there were nonsepeating digits after decimal point.
- In converting repeating decimal fraction into common fraction we have denominator having as many 9s as many repeating digits followed by as many Os as many nonrepeating digits after decimal point. Numerator equals a whole number we get after removing decimal and repeating points in the fraction less the number obtained by deleting the decimal point and all digits in the repeating part.
Remarks: Repeating decimal fractions can always be converted into common fractions. All repeating decimal fractions are rational numbers.
Example 5. Convert 5.23457 into a common fraction.

Explanation: Since there are 5 digits in the decimal part, the repeating decimal fraction has been multiplied by 100000 (5 0s after 1). Since there are two decimal digits before the repeating part (1 followed by 2 Os), repeating decimal fraction has been multiplied by 100.
The second product has been subtracted from the first. On one side of subtraction is a whole number, and in the other the repeating decimal number multiplied by (100000 1000) 99900. Both sides are divided by 99900 to and the common fraction is obtained.
Rules for converting repeating decimal fractions into common fractions =the result by sub tracting
Numerator of the desired fraction the integer obtained by deleting the decimal point of the given decimal fraction and the integer formed by the nonrepeating portion. Denominator of the desired fraction = numbers formed by putting as many 9s as many digits in the repeating part followed by as many Os in the nonrepeating part after the decimal point.
These rules have been applied in the following examples to convert a repeating decimal fractions into common fractions.

Read more:
