Today our topic of discussion is Quadrilateral inscribed in a circle (Inscribed Quadrilaterals).
Quadrilateral inscribed in a circle (Inscribed Quadrilaterals)

Quadrilateral inscribed in a circle (Inscribed Quadrilaterals)
An inscribed quadrilateral or a quadrilateral inscribed in a circle is a quadrilateral having all four vertices on the circle. Such quadrilaterals possess a special property. The following work helps us understand this property
Theorem 23. The sum of the two opposite angles of a quadrilateral inscribed in a circle is two right angles.
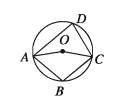
Let ABCD be a quadrilateral inscribed in a circle with centre O. It is required to prove that, ∠ABC + ∠ADC = 2 right angles and ∠BAD+ ∠BCD = 2 right angles.
Drawing: Join O, A and O, C.
Proof:
Step 1. Standing on the same arc ADC, the angle at centre reflex ∠AOC =2( ∠ABC at the circumference)
that is, reflex ∠AOC =2 ∠ABC [The angle subtended by an arc at the centre is double of the angle subtended by it at the circle]
Step 2. Again, standing on the same arc ABC, the angle at the centre ∠AOC = 2 ( ∠ADC at the circumference)
that is, ∠AOC =2 ∠ADC [The angle subtended by an arc at the centre is double of the angle subtended by it at the circle]
∴reflex ∠AOC + angle AOC=2( ∠ABC+ ∠ADC)
But reflex ∠AOC+ ∠AOC = 4 right angles
2( ∠ABC + ∠ADC)=4 right angles
∴∠ABC+∠ADC = 2 right angles
In the same way, it can be proved that ∠BAD+ ∠BCD = 2 right angles. (Proved)
Corollary 6. If one side of a cyclic quadrilateral is extended, the exterior angle formed is equal to the opposite interior angle.
Corollary 7. A parallelogram inscribed in a circle is a rectangle
Theorem 24. If two opposite angles of a quadrilateral are supplementary, the four vertices of the quadrilateral are concyclic.
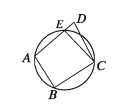
Let ABCD be the quadrilateral with ∠ABC + ∠ADC = 2 right angles. It is required to prove that the four points A, B, C, D are concyclic.
Drawing: Since the points A, B, C are not collinear, there exists a unique circle which passes through these three points. Let the circle intersect AD at E. Join C, E.
Proof: ABCE is a quadrilateral inscribed in the circle.
Therefore, ∠ABC+ ∠AEC = 2 right angles. [The sum of the two opposite angles of an inscribed quadrilateral is two right angles.]
But ∠ABC+ ∠ADC = 2 right angles. [given]
:. ∠AEC = ∠ADC
But this is impossible, since in ΔCED exterior ∠AEC : opposite interior ∠ADC
Therefore, E and D points can not be different points. So, E must coincide with the point D.
Therefore, the points A, B, C, D are concyclic. (Proved)
Read more:
