Rational Fractions

Today is our topic of discussion Rational Fractions .

Rational Fractions

Fraction formed with a polynomial as denominator and a polynomial as numerator is called the rational fraction. For example,

 

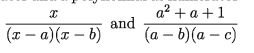
is a rational fraction

partial fractions

If a given fraction is expressed as a sum of two or more fractions, then each of the latter fractions is said to be a partial fraction of the given fraction.

Here the given fraction is expressed as the sum of the two fractions fraction has been divided into two partial fractions.

If both N(x) and D(x) are the polynomials of the variable x and if the degree of numerator N(x) is less than the denominator D(x), then, the fraction is called proper fraction. The degree of numerator N(x) is greater than or equal to that of the denominatorD(x) the fraction is called improper fraction.

 

 

How to convert the proper rational fraction into the partial fraction in different ways is shown below.

1) The denominator is, or can be expressed as a product of distinct linear factors but no factor is repeated.

2) When the degree of the numerator is greater than or equal to that of the denominator, then degree of numerator is lessen by dividing the numerator by the denominator.

3) The denominator is, or can be expressed as a product of linear factors, some of which are repeated.

4) The denominator is or can be expressed as a product of linear and quadratic factor, none of which is repeated.

 

 

5) The denominator is, or can be expressed as a product of linear and quadratic factors, some of which are repeated.

See more:

• Function exercises 1.2
• Prove the total heat gained by an object is equal to the sum of the heat lost by all the surrounding objects