Today is our topic of discussion Relation between two planes.
Relation between two planes
1) If two planes are parallel then they will have no common point.
2) If two planes intersect each other, then they will intersect one another in a straight line and they will have innumerable common points.
Solid
We know that a book, a brick, a box or a spherical ball is a solid and occupies some space. Again, a piece of stone or wood, a part of a brick, a fragment of coal, a lump of dried sticky soil etc are also examples of solids. But these are irregular solids.
The body enclosed by plane or curved surfaces and occupying some space is called a solid. At least three straight lines are required to enclose a portion of a plane, so also four planes are required to enclose some space. These planes are the faces or the surfaces of the solid and the line in which two such planes intersect is an edge of the solid. A book or a brick has six faces and twelve edges. A cricket ball is enclosed by a curved surface.
Volume and area of surface of uniform solids
1. Rectangular Parallelepiped

The solid enclosed by three pairs of parallel planes is called a parallelepiped. Each of the six planes is a parallelogram and the opposite faces are congruent. A parallelepiped has twelve edges divided into three groups.
The parallelepiped of which the faces are rectangles is called a rectangular parallelepiped. The rectangular parallelepiped of which the faces are squares is called a cube. The faces of the rectangular parallelepiped and the faces of the cube in the above diagram are ABCD, A’ * B’ * C’ * D’ BCC’B’, ADD’A’, ABB’A’, DCC’D’ and the edges are AB, A’ * B’ CD, C’ * D’ BC, B’ * C’ AD, A’ * D’ AA’, B * B’ C * C’ D * D’ The only diagonal shown is BD’, the rest have to be drawn.
Let the length, breadth and height of the rectangular parallelepiped be respectively AB = a units, AD = b units and A * A’ = c units.
1) Area of the whole surface
= Sum of the areas of the six faces
= 2 (the area of the face ABCD + the area of the face ABB A+ the area of the face ADD A ) = 2(ab+ac+bc) square units = 2(ab + bc + ca) square units
2) Volume = ABADA * A’ cubic units = abc cubic units
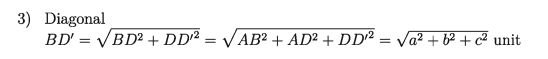
2. Cube
For a cube, a = b = c Therefore,
1) Area of the whole surface = 2(a² + a²+ a²) = 6a² units
2) = a . a . a = a³ cubic units
3) = √a² + a²+ a²) = √3a units
3. Prism
A prism is a polyhedron, bounded by two parallel polygonal faces and the other faces always being parallelograms. The parallel sides are known as bases and the sides are known as lateral faces. If all the lateral surfaces are rectangular it is called a right prism; otherwise they are called oblique prism. Practically right prisms are frequently used. The prism is named by the shape of its base. For example, triangular prism, quadrilateral prism, pentagonal prism etc.
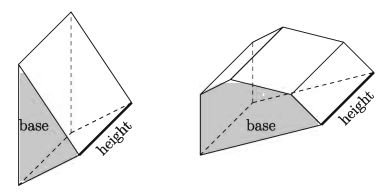
If the base is a regular polygon, the prism is called a regular prism. If the base is not a regular polygon, the prism is known as an irregular prism. So by definition all rectangular solids and cubes are prisms. Right triangular prism made of glass is used for the scattering of light.
1) The area of total surfaces of a prism
= 2 (area of the base) + area of the lateral surfaces
= 2 (area of the base) + perimeter of the base x height
2) volume = area of the base x height
4. Pyramid
A solid figure with a polygonal base and triangular faces that meet at a common point is called a pyramid.

The base of a pyramid is a any polygon and its lateral surfaces are of any triangular shape. But if the base is a regular polygon and the lateral faces are congruent triangles, the pyramid is called regular pyramid. The regular pyramids are eye-catching. The line joining the vertex and any corner of the base is called the edge of the pyramid. The length of the perpendicular from the vertex to the base is called the height of the pyramid. Usually, a solid with a square base and four congruent triangles meeting at a point is considered as a pyramid. These pyramids are in wide use.
A solid enclosed by four equilateral triangles is known as regular tetrahedron which is also a pyramid. This pyramid has 3 + 3 = 6 edges and 4 vertices. The perpendicular from the vertex falls on the centroid of the base.
1) The area of all surfaces of pyramid = Area of the base + area of the lateral surfaces But if the lateral surfaces are congruent triangles,
The area of all surafes of the pyramid = Area of the base+1/2 (perimeter of the base × slant height)
If the height of the pyramid is h, radius of the inscribed circle of the base is r and I is its slant height, then l = √h² + r²
2) volume 1/3 x area of the base x height .
See more:

1 thought on “Relation between two planes”