Today is our topic of discussion Scalar and Vector Quantities.
Scalar and Vector Quantities

Measurement of things is necessary in all spheres of our daily life. Length of a body, measure of time, amount of money, measurement of volume and temperature can be denoted by 5 cm., 3 minutes, 12 taka, 5 litres and 6° C, respectively. For these measurements, it is sufficient to state those quantities with their respective units.
Again, if it is stated that a man starting from a point first travels 4 metres and then 5 metres; then to determine his distance from the starting point, it is necessary to know the direction of his motion. It is not possible to determine correctly how far the man has moved from the starting point unless the exact direction of the motion is known.
The quantity which is completely described by its magnitude with a unit or + or – signs before magnitude is a Scalar Quantity. Length, mass, speed, temperature etc. are scalar quantities.
The quantity which, for its complete description, requires magnitude as well as direction is a Vector Quantity. Displacement, velocity, acceleration, weight, force etc. are vector quantities.
Geometrical interpretation of a vector: directed line segment
If one end of a straight line is termed as the initial point and the other end as the terminal point then the straight line is called a directed line segment. The directed line segment whose initial point is A and terminal point is B is denoted by AB. Each directed line segment is a vector quantity whose measurement is the length of the line segment (represented by (|AB|) or shortly AB) and whose direction is along the line AB straight from A to B.
Conversely, any vector quantity can be expressed by a directed line segment where the length of the line segment is the measurement of the vector quantity and the direction represented from initial point to terminal point is the direction of the vector. Hence, vector quantity and directed line segment are the same. Directed line segments are also called Geometric Vectors. Our discussion will be limited to the vectors in a plane. By vector we shall mean Geometric Vectors.
Any vector (directed line segment) which is a part of an unending straight line is called the support line or just support of the vector. Usually a vector is represented by a letter e.g. u = AB. To denote a vector, the vector is underscored and its directive line segment is adorned with a → above. u = AB means the initial point of the vector u is A and terminal point is B; its direction is from A to B and its length |u| = |AB| is the length of the line segment AB.

Equivalence of vectors and Opposite vector
Equal vector:
A vector u is said to be equal to another vector v if
1) |u| = |v| (Length of u is equal to length of v)
2) Supports of u and v are same or parallel.
3) Directions of u and v are same.
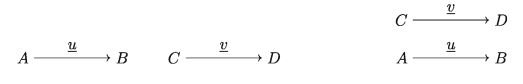
It is easily understood that the definition of equivalence abides by the following rules:
1) u = u
2) If u = v, v = u
3) If u = v and v = w u = w
If the support lines of u and v are same or parallel then we call briefly u and v are parallel.
Note: A vector can be drawn at any point which is equal to a given vector. Because if a point P and a vector u are given, we draw a straight line at the point P which is parallel to support line of u. Now we take PQ line segment to the direction of u and equal to |u| . Then according to the construction, vec PQ = u .

Opposite vector:
v is called the opposite vector of u if
1) |v| = |u|
2) Lines of support of u and v are the same and parallel.
3) The direction of v is opposite of that of u
If v is an opposite vector of u then u is also opposite of v. It is clear from the definition of equality that if both y be the opposite vectors of u then v = w . -u is the opposite vector of u. If underline u = vec AB then – u = vec BA
See more:

1 thought on “Scalar and Vector Quantities”