Lines, Angles and Triangles Exercises 6.3

Today our topic of discussion is Lines, Angles and Triangles Exercises 6.3.

Lines, Angles and Triangles Exercises 6.3

 

Exercises 6.3

1. The lengths of three sides of a triangle are given below. In which case it is possible to draw a triangle (the numbers are in unit of length)?

1) 5, 6, 7

2) 5, 7, 14

3) 3, 4, 7

4) 2, 4, 8

2. If one side of a equilateral triangle is produced to both, sides then what is difference between the generated exterior angles??

1) 0°

2) 120°

3) 180°

4) 240°

 

 

3. In figure what is the value of ∠RPS ?

1) 40°

2) 70°

3) 90°

4) 110°

4. In the adjacent figure

 

 

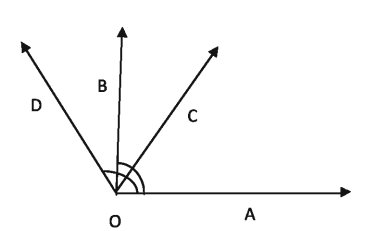
(i) ∠AOC is an acute angle

(ii) ∠AOB is a right angle

(iii) ∠AOD is a reflex angle

Which one of the following is correct?

1) i

2) i

3) i and ii

4) ii and iii

5. If a triangle when placed on another exactly covers the other

(i) the two triangles are congruent

(ii) the corresponding sides of the two triangles are equal

(iii) corresponding angles are equal

Which one of the following is correct?

1) i, ii

2) i, iii

3) ii, iii

4) i, iian * diii

 

 

In the above figure AB||EF|| * CD and BD perp CD Answer the questions

(68) based on the given figure:

6. What is the value of ∠AEF?

1) 30°

2) 60°

3) 240°

7. Which one of the following is the value of ∠BFE?

1) 30°

2) 60°

3) 90°

4) 270°

8. ∠CEF+∠CEG = what?

1) 60 °

2) 120°

3) 180 °

4) 210°

9. Prove that, the triangle formed by joining the mid points of the sides of an equilateral triangle is also equilateral.
10. Prove that, the three medians of an equilateral triangle are equal.
11. Prove that, the sum of any two exterior angles of a triangle is greater than two right angles.
12. In triangle ABC , D is the mid point of side BC. Prove that, AB + AC > 2AD
13. In the figure given, ∠C = 1 right angle and ∠B = 2∠A. Prove that, AB = 2BC
14. Prove that, the exterior angle so formed by producing any side of a triangle is equal to the sum of the interior opposite angles.
15. Prove that, the difference between any two sides of a triangle is less than the third.
16. In the figure, in triangle ABC, ∠B = 1 right angle and D is the mid point of hypotenuse AC. Prove that, BD = 1/2 * AC
17. In Δ ABC ,AB > AC and bisector of ∠A is AD which intersects side BC at point D. Prove that, ∠ADB is obtuse angle.
18. Prove that, any point on the perpendicular bisector of a line segment is equidistant from the terminal points of that line segment
19. In triangle ABC, ∠A = 1 right angle. Mid point of BC is D 

1) Draw a triangle ABC with given information.

2) Show that, AB + AC > 2AD

3) Prove that, AD = 1/2 * BC

20. In Δ ABC , D and E are the mid points of AB and AC respectively and bisectors of ∠B and ∠C intersect at point O.

1) Express the information of the stem through figure.

2) Prove that, DE || BC and DE = 1/2 * BC

3) Prove that, ∠BOC =90° + 1/2 ∠ A

21. Prove that, bisector of the vertical angle of an isosceles triangle bisects the base and perpendicular to base.
22. Prove that, sum of the three medians of a triangle is less than the perimeter of the triangle.
23. An industrious father called upon his only son and said that he hid gold in a nearby forest which he bought with his earned money. When the son asked about the position of the gold, he informed him that there were two similar trees A and B and a stone S. After reaching from S to A, he would have to go perpendicularly the same distance to find the point C. Again coming from S to B, he would have to travel the same distance perpendicularly to find the point. D. Then he would find the gold at the midpoint of the line CD. The son found the trees A and B but unfortunately did not find S. Will the son able to find the gold? If so, then how?

 

 

Read more:

• Solving Linear Equations
• Principle of calorimetry